Задачи и системы адаптивного управления, страница 13

Система подготовки перегретого пара имеет установившиеся режимы работы при разных (но фиксированных) значениях нагрузки. Эти режимы установятся, если входной сигнал регулятора  является сигналом с ограниченной энергией.

5.2. Алгоритм формирования управляющего воздействия

Функционал обобщенной работы системы управления. Множество допустимых входных сигналов разомкнутой системы управления (21), (22) содержит вектор входных сигналов регулятора

 ,

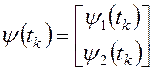обращающих в минимум функционал обобщенной работы

,

где:  - допустимая погрешность управления;

 - предел основной погрешности измерений расхода воды;

 - предел основной погрешности измерений сигнала ;

 - весовой коэффициент (параметр регуляризации), величину которого выбирают из диапазона ;

.

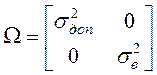Задачу оптимизации этогоквадратичного функционала обобщенной работы с ограничениями, создаваемыми разностным уравнением состояния (21) (задачу условной оптимизации), решают с помощью принципа максимума в следующей  последовательности [23]:

1). С помощью вектора неопределенных множителей Лагранжа  преобразуют задачу условной оптимизации в задачу безусловной оптимизации следующей функции Гамильтона:

 

.

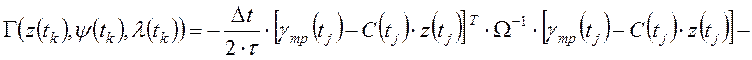
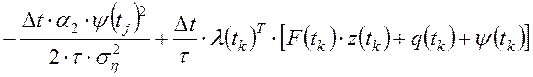2). Из необходимых и достаточных условий минимума функции Гамильтона получают уравнения Эйлера-Лагранжа:

;

;

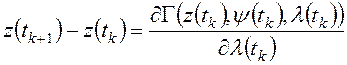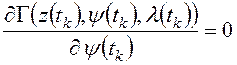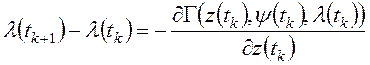
и краевые условия в начальный   и конечный   моменты времени

;  .

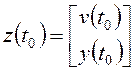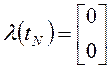3). Из этих уравнений Эйлера-Лагранжа с помощью принципа максимума и инвариантного погружения получают следующий рекуррентный алгоритм определения переменных состояния замкнутой системы управления:

      

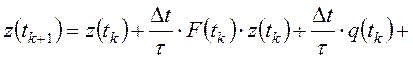
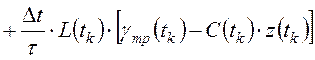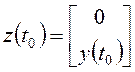                  ;     ;                       (23)

;     ,

(24)

где используется матрица

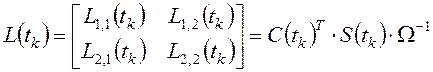.                                          (25)

Алгоритм управления. Приближенно (с точностью до погрешностей измерений) должны выполняться следующие равенства:

.

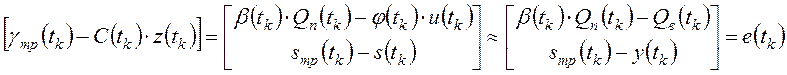Поэтому матричное уравнение (23) можно представить в виде системы уравнений:

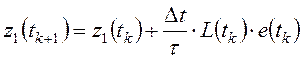           ;      ;                                         (26)

               ;     .                                             

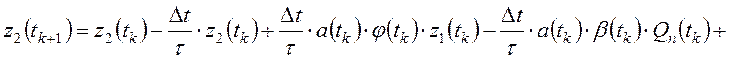
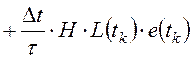С другой стороны процесс изменения уровня в барабане котла описывает уравнение (2):

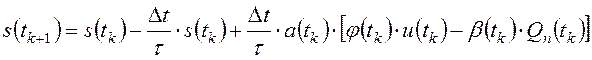;  .   (f)

Из последних двух уравнений следует, что их правые части будут равны между собой (по условию ), если

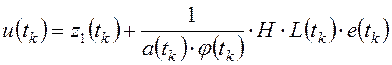.                                                 (27)

Таким образом, уравнения (23)-(27) образуют рекуррентный алгоритм формирования управляющего воздействия .

Для удобства практической реализации этого алгоритма объединим уравнения (23)-(27) в одну систему уравнений:

;    ;        ;     , где: ; ;                          ;      .

(28)

Анализ алгоритма управления. Уравнения (28) образуют алгоритм многомерного ПИ-регулятора с перенастраиваемыми параметрами (с двумя входными воздействиями, объединенными в вектор ).

Матрица Гессе 

,

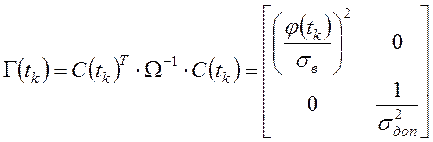входящая в уравнение (28), положительно определена при любых значениях функции . Кроме того, разомкнутая система управления (21), (22) наблюдаема и управляема по входу . Поэтому полученный алгоритм управления (28) линейным объектом (2) асимптотически устойчив [10].

Разомкнутая система управления (21), (22) наблюдаема и управляема по входу , а входное воздействие  - сигнал с ограниченной энергией. Поэтому система управления с ПИ-регулятором (27) - астатическая [23].

Другие частные показатели качества управления можно определить моделированием на ЭВМ переходных процессов в системе управления.

5.  Моделирование переходных процессов в цифровой системе          адаптивного управления уровнем пароводяной смеси в барабане котла

Анализ эффективности системы управления, реализующей алгоритмы обучения модели объекта управления (16) и формирования управляющего воздействия (27) выполнен моделированием на ЭВМ переходных процессов в разработанной системе управления. При моделировании использовались результаты измерений сигналов штатной системы подготовки перегретого пара (рис. 2), представленные на рисунках (3)-(6).