Случай на рис.1.6.г отвечает изолятору. Первая энергетическая зона в этом случае полностью заполнена, а вторая зона, отделенная от первой большим энергетическим разрывом, полностью свободна. В кристаллах с таким энергетическим спектром электрическое поле не может разгонять электроны. Такой кристалл будет обладать свойствами диэлектрика, хотя в нем так же, как и в металле, имеется значительное количество коллективных электронов.
1.5. Зонная теория полупроводниковых материалов
Электронный спектр полупроводника близок к изолятору (рис.1.6.г). Первая энергетическая зона полностью заполнена, а вторая, отделенная от первой, полностью пуста. Однако величина энергетического разрыва между зонами значительно меньше, чем у изолятора. За счет термического, светового или другого возбуждения электроны первой зоны могут перебрасываться во вторую, благодаря чему кристалл приобретает способность проводить электрический ток.
Переброс определенного количества электронов в верхнюю, ранее пустую, зону освобождает такое же количество электронных состояний в нижней, ранее полностью заполненной зоне. Эти пустые электронные состояния можно трактовать теперь как дырки в энергетическом спектре кристалла. Появление дырок в первой зоне также обуславливает перенос электричества в результате смещения дырок на более низкие уровни и обмена местом с электроном, находящимся на этих уровнях.
Следовательно, перенос электричества в полупроводниках может осуществляться как электронами, переброшенными в пустую зону, так и дырками в заполненной зоне. В связи с этим дырочную проводимость необходимо рассматривать как перемещение дырок, которое соответствует движению частиц с эффективной массой и зарядом, равным заряду электрона, но обратного знака. В связи с двойным механизмом переноса электричества в полупроводниках рассматриваются два вида проводимости. Во второй зоне проводимость обеспечивается обычными электронами и называется электронной проводимостью (обозначается Δn-), а в первой заполненной зоне перенос заряда обеспечивается перемещением дырок с эффективным положительным зарядом – дырочная проводимость (обозначается Δn+). По виду проводимости полупроводниковые материалы делятся на две группы: полупроводники Δn- и Δn+ типов.
Электропроводность полупроводниковых материалов зависит от количества электронов в зоне проводимости и дырок, а также их подвижности. Поэтому электропроводность полупроводников (γ) в отличие от металлов с повышением температуры растет по закону, описываемому уравнением Аррениуса
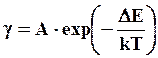(1.18)
где А – коэффициент, связанный с природой полупроводников.
Полупроводниковые материалы, проводимость которых зависит только от числа носителей тока и их подвижности, обусловленной температурой кристалла, называют собственными, а их проводимость - собственной проводимостью. Это связано с тем, что механизм появления электронов проводимости и дырок определяется только собственного энергетического спектра и не связан с примесями.
Увеличение числа носителей тока может быть связано также с дефектами кристаллического строения. Нарушение атомной структуры кристалла, в том числе нарушения типа вакантных узлов и дислоцированных атомов вследствие деформации и наличия примесей приводит к искажению и появлению дефектов в картине энергетического спектра кристалла. Полупроводники, в которых концентрация носителей тока обусловлена примесями, называют примесными полупроводниками.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.