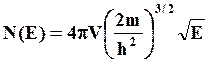Электронное строение материала. Квантовая теория свободных электронов. Зонная теория металлов, страница 5

                                                                   (1.13)

Произведение N(E)dE представляет собой количество квантовых состояний  в единице объема металла, которое приходится на интервал энергий между Е и Е+dE. Другими словами это произведение равно числу электронов, которое заполняет указанный интервал. Из рис. 1.3 следует, что чем больше энергия электронов, тем больше плотность энергетических состояний.

В соответствии с принципом Паули при Т = 0^оК электроны занимают все возможные наиболее низкие энергетические состояния, и так как при указанной температуре нет электронов с энергией, превышающих максимальную энергию свободных электронов, то плотность N(E) будет ограничена условием Е = Е_max

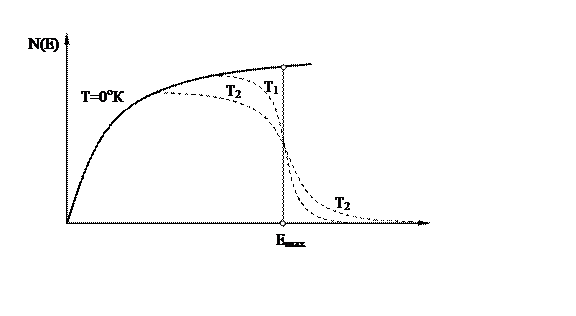
Рис.1.3. Распределение электронов но энергетическим состояниям

Общее число электронов с энергиями от 0 до Е_max  графически равно площади под кривой N(E), тогда суммарная энергия всех свободных электронов находится из уравнения

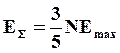                                                                                    (1.14)

откуда следует, что средняя энергия одного электрона при Т =0^оК составляет 3/5 от Е_max. Средняя энергия свободных электронов даже при абсолютном нуле довольно высока, что является прямым следствием принципа Паули, который, исключает пребывание в одном энергетическом состоянии более двух электронов с противоположными спинами.

Определим длину волны электронов, обладающих максимальной энергией на поверхности сферы Ферми. Значение длины волны можно найти из выражения, представляющее решение уравнения Шредингера для электрона в одномерной потенциальной яме

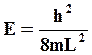                                                                                      (1.15)

где m – масса электрона; h – постоянная Планка; L – ширина потенциальной ямы.

При n = 1 и λ = 2L получим

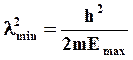                                                                                  (1.16)

А с учетом значения Е_max  окончательно получим

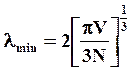                                                                                            (1.17)

Расчеты показывают, что для одновалентных металлов длина волны λ_min  составляет примерно удвоенное межатомное расстояние.

1.4. Зонная теория металлов

Рассмотрим основные положения зонной теории металлов. Металлы в твердом состоянии имеет кристаллическое строение, характеризующееся правильным расположением ионов в узлах решеток. Так как ионы обладают положительным зарядом, то в бездефектной структуре они создают периодическое поле, представляющее собой последовательный ряд одинаковых потенциальных ям и барьеров. Характер движения электронов  в таком поле зависит от соотношения их кинетической энергии и глубины потенциального барьера.

Если кинетическая энергия электронов намного меньше высоты потенциальных барьеров, разделяющих ямы, то барьеры становятся практически непроницаемыми для электронов. В этом случае обеспечивается сильная связь электрона со своим ядром атома. Волновые функции таких электронов представляют стоячие волны, ограниченные размерами потенциальной ямы. Энергия таких электронов квантована, энергетический спектр дискретен, отсутствует взаимодействие между электронами соседних атомов, а энергетические уровни таких электронов одинаковы.

Если кинетическая энергия электронов превышает высоту потенциального барьера, т.е. энергия взаимодействия электронов с ионами кристаллической решетки меньше кинетической энергии самих электронов. В этом случае электроны рассматриваются как свободные, а волновые функции таких эле кронов представляют бегущие волны, энергетический спектр которых непрерывен.

Усиление связи приводит к усилению периодического возмущения движения электронов и вызывает появление разрывов в энергетическом спектре с разделением его на отдельные полосы – зоны. Дальнейшее усиление связи приводит к захвату ионами электронов и вырождению энергетических полос в линейчатые уровни.