Квантовая механика базируется на математической теории вероятности. Принципиальное ее отличие от классической состоит в том, что квантовая механика позволяет определить лишь вероятность события, например нахождения частицы в данной точке пространства в конкретное время. В основе квантовой теории лежит уравнение Шредингера, описывающее движение микрочастиц в эквипотенциальных энергетических полях, в том числе и электронов. Энергетический спектр квантовых частиц дискретен и состоит из отдельных уровней, при этом энергия электрона в энергетическом поле атома также квантована.
В основе квантовой теории свободных электронов лежит рассмотрение общего случая поведения электрона в трехмерном пространстве. Допустим, что имеем объем металла в виде куба с длиной ребра L и объемом V = L3, в котором по всем направлениям свободно движутся коллективизированные электроны. Согласно принципу неопределенности точное нахождение импульса или энергии электрона накладывает неопределенность на положение электрона в твердом теле, которая в любом направлении будет равна размеру кристалла в этом направлении.
При переходе к трехмерному пространству если неопределенность в направлении каждой оси составляет h/L, то для куба со стороной L она в изменении импульса каждого состояния будет равна
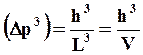(1.10)
и может быть представлена в трехмерном (фазовом) пространстве в виде минимального объема: h3/V. В связи с этим все пространство импульсов, связанное со значениями энергии, можно представить как состоящим из маленьких ячеек с длиной ребра h/L и объемом h3/V.
Каждая такая ячейка представляет собой одно из возможных квантовых электронных состояний, к которым применим принцип Паули. Это означает, что в каждом квантовом состоянии могут находиться максимум два электрона с противоположными спинами. Последнее в свою очередь означает, что все электроны при Т = 0оК не могут собраться в начале координат, т.к. в этом случае в ячейке, соответствующей началу координат, содержалось бы более двух электронов. Следовательно, при абсолютном нуле энергия электронного газа не может быть равна нулю.
Принцип Паули требует, чтобы при абсолютном нуле N электронов в объеме V занимали N/2 уровней от Еmin до Еmax, при этом будут заполнены те уровни, которым соответствует минимальная энергия. Последнее требует симметричного заполнения уровней относительно начала координат в пространстве импульсов, а занятые состояния образуют сферу с центром в начале координат (рис. 1.2), которая названа сферой Ферми.
Рис. 1.2. Пространство импульсов электронного энергетического состояния
Внутри сферы Ферми энергия убывает о поверхности к центру, а граница сферы отвечает максимально возможной энергии электронов при абсолютном нуле температуры. Кинетическая энергия электронов внутри сферы возрастает пропорционально квадрату расстояния, т.к. импульс пропорционален радиусу, а полная энергия равна
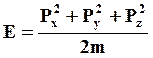(1.11)
Все электроны, значения импульсов которых лежат на поверхности сферы радиусом r1, имеют одинаковую энергию, и им отвечает максимальный импульс.
Объем всех занятых уровней-ячеек внутри сферы Ферми можно найти из соотношения
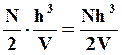
Так как Pmax соответствует радиусу границы сферы Ферми, то объем занятых ячеек будет равен
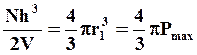
откуда
следует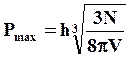 
Из (1.11) следует, что при Т =0оК
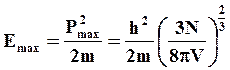(1.12)
где N – число свободных электронов в металле объемом V.
Свойства совокупности свободных электронов зависят от их распределения по энергетическим состояниям и характеризуется кривой N(E), которая определяет плотность электронов с энергией Е. Для свободных электронов эта кривая описывается уравнением (1.13) и имеет вид параболы (рис. 1.3)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.