Состояние коллективизированных электронов в зонной теории металлов, в отличие от теории свободных электронов, описывается не в пространстве импульсов, а в пространстве волновых векторов. Связь между импульсом и волновым вектором можно получить из соотношения де Бройля
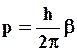
где β – волновой вектор, который по направлению совпадает с импульсом и прямопропорционален ему по величине.
В реальных кристаллах электронный газ не является полностью свободным. На движение электронов существенное влияние оказывает периодически меняющееся поле решетки, в результате чего энергетические уровни свободных электронов расщепляются в почти непрерывные энергетические зоны. На рис. 1.4 показано возможное изменение потенциальной энергии поля решетки, воздействующее на электрон при его перемещении вдоль оси X, проходящее через цепочку равностоящих друг от друга ионов, размещенных в узлах кристаллической решетки. Как видно из рисунка потенциальная энергия U(x) представляет периодическую функцию с периодом, равным параметру решетки d.
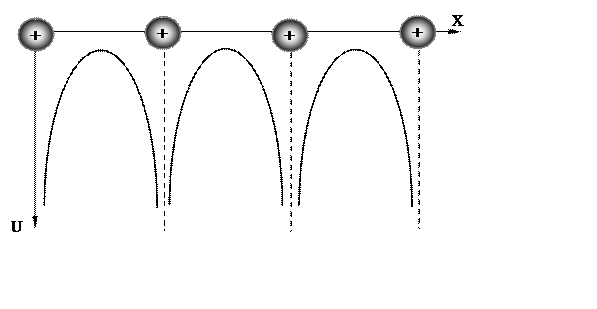
Рис. 1.4. Характер изменения потенциальной энергии поля кристаллической решетки металла, воздействующей на электрон при его перемещении
Анализ уравнения Шредингера для частицы, движущейся в периодическом поле, показывает, что периодически изменяющееся поле приводит к разрыву энергетического спектра на энергетические зоны с разрешенными и запрещенными значениями энергий. Если поле U(x) = 0, зоны запрещенных значений исчезают. При сильной связи электрона и ядром атома из-за периодичности поля будет иметь место совокупность совершенно изолированных потенциальных ям.
При переходе от сильной к более слабой связи электроны попадают в промежуточное состояние, при котором вместо непрерывной зависимости энергии от волнового вектора получается зависимость в виде отдельных зон. Эти зоны состоят из отдельных уровней, число которых равно числу потенциальных ям, т.е. числу ионов в узлах кристаллической решетки. Каждый уровень представляет одно квантовое состояние, на котором, согласно принципу Паули, могут находиться два электрона с противоположно ориентированными спинами. Поэтому при N квантовых состояниях в зоне (N – число ионов в кристаллической решетке) число электронов, которые могут находиться в ней, зависит от характера зоны. В s-зоне может находиться 2N электронов в p-зоне – 6N электронов и т.д.
Влияние периодичности поля кристаллической решетки приводит к возникновению значений энергии электронов, при которых они перестают быть свободными. При этом электроны испытывают колебательное движение, что сказывается на разрыве зависимости энергии от волнового числа. Зоны разрыва называют энергетический щелью и представляют запрещенные области. Запрещенные и разрешенные зоны могут быть представлены в виде диаграмм в двух и трехмерном пространстве. В этом случае они называются зонами Бриллюэна.
На границах зоны происходит разрыв энергетического спектра, однако в зонах могут быть направления, по которым возможно соприкосновение и даже перекрытие зон. В результате этого энергетический спектр частицы оказывается квазинепрерывным. Перекрытие зон происходи только в том случае, когда минимальная энергия нижней границы второй зоны оказывается меньше максимальной энергии верхней границы первой зоны. В противном случае перекрытия зон не происходит.
Каждая зона содержит ограниченное число квантовых состояний, а в соответствии с принципом Паули в каждом таком состоянии может находиться не более двух электронов с противоположными спинами. При ограниченном количестве электронов в твердом теле заполнена будет только часть состояний. Если электронные состояния однородно распределены в пространстве сферы Ферми, то их распределение по энергиям неоднородно и характеризуется кривой N(E). В случае свободных электронов она имеет вид параболы, представленной на рис. 1.3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.