При выводе выражения (1.3) предполагается, что электрон теряет добавочную скорость каждый раз, как только он испытывает столкновение с узлом решетки, и вновь ее приобретает под действием поля.
Предполагая, что средняя скорость электронов значительно превосходит добавочную, т.е. υср >> u, время свободного τ пробега при известной длине свободного пробега (L) можно представить
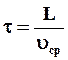
![]() (1.4)
(1.4)
С учетом (1.3) и (1.4) выражение (1.2) примет вид
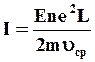 (1.5)
(1.5)
Из (1.5) следует
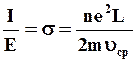 (1.6)
(1.6)
Отношение силы тока к напряженности электрического поля называется электропроводностью (σ), а обратная величина этого выражения - электросопротивлением
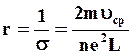
![]() (1.7)
(1.7)
Подставив в выражение (1.7) значение средней скорости (1.1), получим
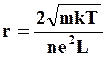 (1.8)
(1.8)
Из (1.8) следует, что электросопротивление тем меньше, чем больше свободных электронов в единице объема и чем больше средняя длина свободного пробега L. Если принять длину L равной межатомному расстоянию порядка ~ 10-8см, то имеет место хорошее совпадение расчетных и экспериментальных значений электропроводности и электросопротивления.
На основе классической электронной теории металлов находит объяснение закон Видермана-Франца, согласно которому отношение теплопроводности металла к его электропроводности представляет универсальную величину, не зависящую от природы металла
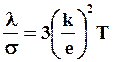 (1.9)
(1.9)
Классическая теория металлов хорошо объясняет оптические свойства металлов. В соответствии с этой теорией при падении луча света на металл свободные электроны могут колебаться в переменном электромагнитном поле, возникающем в металле под действием светового луча. При этом электрон поглощает энергию луча и тем самым делает металл непрозрачным. Сам же электрон, находясь в возбужденном состоянии, стремится вернуться на более низкие энергетические уровни, испуская при этом энергию. Таким образом, за счет обмена энергией между квантом света и электроном световой луч будет полностью отражаться от металла, вследствие чего появится блеск.
Однако классическая теория обладает рядом недостатков, в частности, она не объясняет температурной зависимости электросопротивления, а также не в полной мере раскрывает теплоемкость электронного газа.
1.3. Квантовая теория свободных электронов
Квантовая электронная теория металлов, так же как и классическая теория, исходит из допущения существования свободных электронов. Согласно волновым представлениям, свободно движущийся электрон описывается плоской монохроматической волной. Если длина волны превышает удвоенное межатомное расстояние, то в неискаженной решетке такая волна распространяется без рассеяния и отражается на поверхности металла. В стационарном состоянии в металле образуется система плоских стоячих волн, подобно системе акустических волн, образующих дискретный спектр. Вследствие большого диапазона частот и большой густоты их расположения этот спектр можно рассматривать как квазинепрерывный и образующий энергетическую полосу конечной ширины (по ширине не превышающий значение внутреннего потенциала решетки).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.