Министерство образования Российской Федерации
на тему
Варианты заданий и методические указания к курсовой работе
для студентов факультета АВТ специальностей 210100 и 220400 всех форм обучения
2003 г.
Курсовая работа посвящена решению линейного обыкновенного дифференциального уравнения второго порядка с постоянными коэффициентами (задача Коши) методом Адамса четвертого порядка точности с прогнозом и коррекцией решения и с вычислением решения в первых двух точках методом Рунге-Кутта четвертого порядка точности.
Полученное численным методом решение дифференциального уравнения сравнивается с истинным решением, представленным в аналитическом виде, с целью определения погрешностей получаемых в процессе решения дифференциального уравнения.
Целью курсовой работы является приобретение навыков использования алгоритмов вычислительной математики, организации вычислительных процессов на ЭВМ с использованием библиотеки прикладных программ, анализа и оценивания получаемых результатов.
Материалы выполнения курсовой работы оформляются в виде пояснительной записки к курсовой работе.
1. Постановка задачи
На
интервале 
решить дифференциальное уравнение
с шагом 
методом Адамса
четвертого порядка точности с прогнозом и коррекцией решения.
Определить
на погрешности численной процедуры метода
Адамса, для чего необходимо сравнить полученное решение 
с
точным 
, 
,
вычисленным аналитически. Уравнение второго порядка с правой частью 
имеет решение
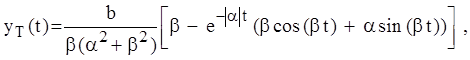
где 
и 
-
вещественная и мнимая части корней характеристического уравнения
Проанализировать
влияние шага решения дифференциального уравнения на точность
решения, для чего необходимо изменить параметр от 
до 
c шагом 
Варианты задания приведены в таблице.
Таблица
|
№ п/п |
T |
|
k |
|
|
|
|
|
1 |
10,0 |
0,0 |
10,0 |
[0; 160] |
0,5 |
2,5 |
0,5 |
|
2 |
10,0 |
0,1 |
10,0 |
[0; 160] |
0,5 |
2,5 |
0,5 |
|
3 |
10,0 |
0,2 |
10,0 |
[0; 160] |
0,5 |
2,5 |
0,5 |
|
4 |
10,0 |
0,3 |
10,0 |
[0; 150] |
0,5 |
2,5 |
0,5 |
|
5 |
10,0 |
0,4 |
10,0 |
[0; 140] |
0,5 |
2,5 |
0,5 |
|
6 |
10,0 |
0,5 |
10,0 |
[0; 130] |
0,5 |
2,5 |
0,5 |
|
7 |
10,0 |
0,6 |
10,0 |
[0; 120] |
0,5 |
2,5 |
0,5 |
|
8 |
10,0 |
0,7 |
10,0 |
[0; 110] |
0,5 |
2,5 |
0,5 |
|
9 |
10,0 |
0,9 |
10,0 |
[0; 100] |
0,5 |
2,5 |
0,5 |
|
10 |
5,0 |
0,3 |
5,0 |
[0; 80] |
0,2 |
1,0 |
0,2 |
|
11 |
5,0 |
0,5 |
5,0 |
[0; 70] |
0,2 |
1,0 |
0,2 |
|
12 |
5,0 |
0,6 |
5,0 |
[0; 65] |
0,2 |
1,0 |
0,2 |
|
13 |
5,0 |
0,7 |
5,0 |
[0; 60] |
0,2 |
1,0 |
0,2 |
|
14 |
5,0 |
0,9 |
5,0 |
[0; 50] |
0,2 |
1,0 |
0,2 |
|
15 |
2,0 |
0,0 |
2,0 |
[0; 32] |
0,1 |
0,5 |
0,1 |
|
16 |
2,0 |
0,1 |
2,0 |
[0; 32] |
0,1 |
0,5 |
0,1 |
|
17 |
2,0 |
0,2 |
2,0 |
[0; 32] |
0,1 |
0,5 |
0,1 |
|
18 |
2,0 |
0,6 |
2,0 |
[0; 24] |
0,1 |
0,5 |
0,1 |
|
19 |
2,0 |
0,8 |
2,0 |
[0; 20] |
0,1 |
0,5 |
0,1 |
|
20 |
1,0 |
0,0 |
1,0 |
[0; 14] |
0,05 |
0,09 |
0,01 |
|
21 |
1,0 |
0,2 |
1,0 |
[0; 12] |
0,05 |
0,09 |
0,01 |
|
22 |
1,0 |
0,4 |
1,0 |
[0; 10] |
0,05 |
0,09 |
0,01 |
|
23 |
0,5 |
0,0 |
50,0 |
[0; 12] |
0,05 |
0,09 |
0,01 |
|
24 |
0,5 |
0,2 |
50,0 |
[0; 12] |
0,05 |
0,09 |
0,01 |
|
25 |
0,5 |
0,4 |
50,0 |
[0; 10] |
0,05 |
0,09 |
0,01 |
|
26 |
0,5 |
0,8 |
50,0 |
[0; 6] |
0,05 |
0,09 |
0,01 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
