Решение дифференциального уравнения: Варианты заданий и методические указания к курсовой работе, страница 2

2. Основные теоретические положения

            Из численных методов решения линейных обыкновенных дифференциальных уравнений чаще всего на практике используют алгоритмы Рунге-Кутта и Адамса четвертого порядка точности с прогнозом и коррекцией решения.

            Пусть необходимо отыскать решение дифференциального уравнения вида

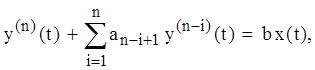
                                                        (2.1)

     Учитывая, что  где  - шаг дискретизации по времени, а  выражение (2.1) запишем в виде

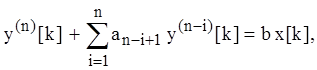
                                     (2.2)

   Численная реализация метода Рунге-Кутта четвертого порядка точности:

1)  для -го момента времени определяются коэффициенты   

                       …

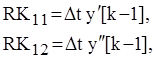
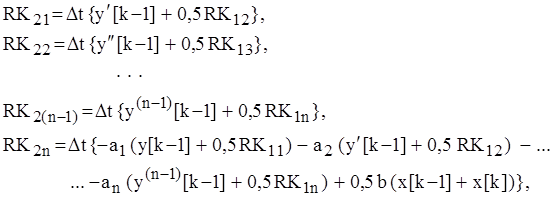
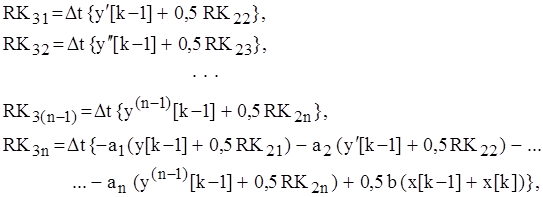
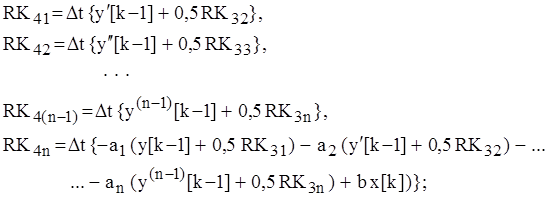
2) для -го момента времени определяются решение и его производные

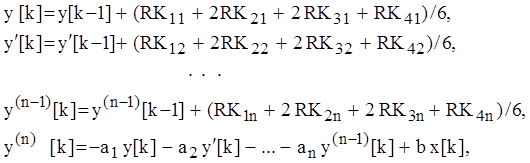
при   

Описанный алгоритм реализован в подпрограмме N1YRKC (см. приложение).

Численная реализация метода Адамса четвертого порядка точности с прогнозом и коррекцией решения:

1) для -го момента времени явным методом Адамса третьего порядка точности вычисляется прогноз решения и его производных

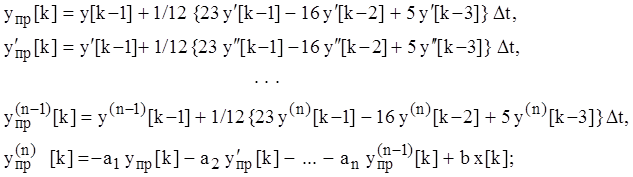
2) для -го момента времени неявным методом Адамса третьего порядка точности производится  коррекция решения и его производных

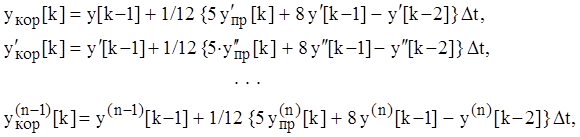
3)  для -го момента времени определяется решение и его производные

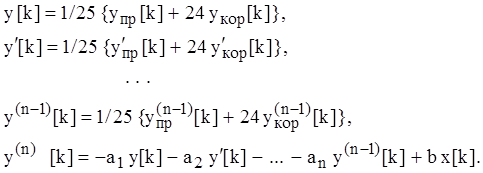
Последняя операция позволяет повысить порядок точности описанного комбинационного алгоритма на единицу, поскольку при суммировании погрешности явного и неявного алгоритмов, имеющие противоположные знаки, частично приводятся.  

Данный комбинационный алгоритм реализован в подпрограмме N1YADC (см. приложение). Метод Адамса значительно проще реализуется на ЭВМ и, следовательно, при решении дифференциального уравнения на длительном интервале времени меньше накапливает вычислительные погрешности. Однако решение методом Адамса в -й момент времени определяется через известные решения в (- 1)-й, (- 2)-й и (- 3)-й моменты времени (в общем случае количество точек с известными решениями зависит от порядка точности метода Адамса). Таким образом, начать процедуру решения дифференциального уравнения методом Адамса четвертого порядка точности нельзя.

От этого недостатка свободен метод Рунге-Кутта, в том числе и четвертого порядка точности, согласно которому решение в -й момент времени определяется через решение только в (- 1)-й момент. Но реализация метода Рунге-Кутта четвертого порядка точности гораздо сложнее метода Адамса (из-за вычисления коэффициентов RK на каждом шаге решения), а, следовательно, он в большей степени может накапливать вычислительные погрешности на длительных интервалах решения. Поэтому целесообразно использовать сочетание этих алгоритмов. Решение начинают методом Рунге-Кутта, определяют решение в необходимом числе точек, а затем продолжают методом Адамса. Указанный способ реализован в подпрограмме N1YDUA (см. приложение).

Результирующая погрешность численного решения дифференциального уравнения в курсовой работе складывается из двух составляющих: методической, что обусловлено соответствующим выбором шага решения  при выбранном порядке точности алгоритма и вычислительной (полагаем, что исходные данные заданы точно).

Оценивать погрешности численного решения дифференциального уравнения следует так же, как и при решении задачи аппроксимации (см. выражения (1.15), (1.16)).

3. Порядок выполнения работы

Ознакомиться с теоретическими положениями в методических указаниях к данному заданию и описанием пакетом прикладных программ (см. приложение), необходимых для его выполнения.

В соответствии с вариантом определить коэффициенты дифференциального уравнения и записать аналитическое выражение точного решения  (см. раздел 1).

Составить на алгоритмическом языке Фортран программу решения дифференциального уравнения и анализа влияния шага решения  на точность решения, для чего необходимо:

·  осуществить ввод исходных данных;

·  вычислить реализацию точного решения  на интервале  с заданным ;

·     вычислить реализацию решения дифференциального уравнения методом Адамса на интервале  с шагом  (осуществляется с помощью подпрограммы N1YDUA);

·     вычислить погрешности решения дифференциального уравнения численным методом (осуществляется с помощью подпрограммы N1YEEE);

·  повторить вычисления для всех  согласно варианту.