Методика применения пакета Mathcad для решения научных и типовых общетехнических задач, страница 7

2. Вычисления по формулам

·  Переменных аргументов в виде отрезков рядов – 10 и более (см. рис.1.1).

·  Количество строк в таблице расчета (выходной таблице) по формуле (1.1) рис.1.1 равно: х × h × l × а1× s × n × а3 × а4 × а6 × n1 = 11 × 4 × 4 × 2 × 3 × 3 × 4 × 4 ×4 × 3 = 6,083 × 10⁵  (более 600 тыс.).

·  Время вычисления по формуле (1.1) – 6,2 c /5,66 c (здесь и ниже: по экранному секундомеру/ с использованием функции time(…)).

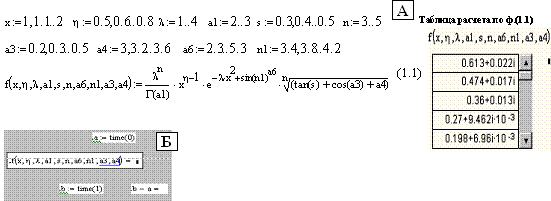
Рис. 1.1. Элементы вычисления по формуле (1.1) в Mathcad:                                                                                       А – простые, Б – с оценкой времени посредством функции time(…)                                                                (фрагмент показан перед запуском вычислений и оценкой их времени нажатием клавиши F9)

2. Решение полиномиального уравнения

·  Порядок уравнения – больше 22.

·  Время решения уравнения 22-го порядка (1.2) рис.1.2 – < 0,5 c/0,063 с.

 

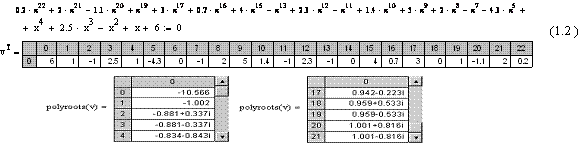Рис. 1.2. Элементы вычисления корней полиномиального уравнения (1.2) в Mathcad

v^T – вектор коэффициентов уравнения; polyroots (v) – функция вычисления корней (фрагменты          ее таблицы с вычисленными корнями – 22 шт.)

3. Решение алгебраических и трансцендентных уравнений и их систем, систем линейных уравнений, оптимизация на «системах уравнений» с использованием решающего блока Given …решающая функция

 Порядок решаемых уравнений и систем – до 400 [8]; системы линейных уравнений могут иметь до 8192 ограничений, а нелинейных – до 200. При установке умощняющего пакета «Solving and Optimization Extension Pack» упомянутые величины увеличиваются в несколько раз, например, для систем квадратных уравнений число переменных можно увеличить до 1000.

4. Решение линейного дифуравнения

·  Порядок решаемого дифуравнения: для Mathcad 2001– больше 33 (см. рис. 7.1 Пособия), для Mathcad 12 и 13 – больше 43 (для решателя rkfixed(…)) и не более 5 (для решателя odesolve(…)).

·  Время решения дифуравнения 8-го порядка из рис.1.3 с построением таблицы вычислений в 6000  строк и графика – 0,079 с.

 

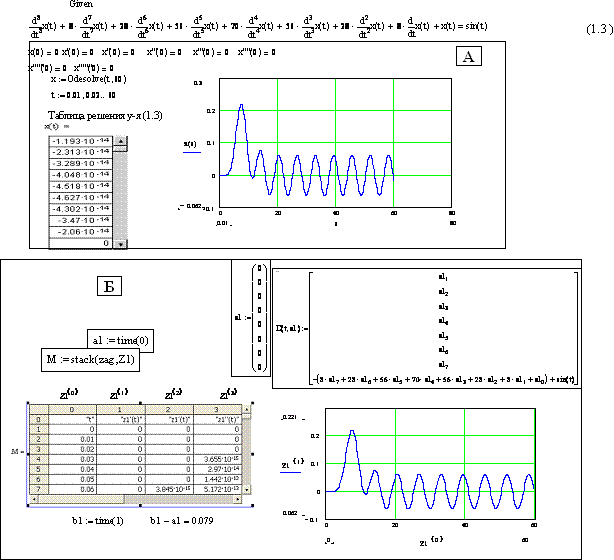
Рис. 1.3. Элементы решения дифуравнения (1.3) с таблицей и графиком:                                                         А – решателем odesolve(…) в Mathcad 2001; Б – rkfixed(…) в Mathcad 13                                                                      для компьютера разд.3 (а1 и b1 – элементы применения функции time(…))

5. Дифференцирование

Порядок производной: прямое дифференцирование – до 5; вложенное дифференцирование – 6 и более: ограничено погрешностью вычисленной производной – первая производная получается с 7 – 8 значащими цифрами, каждое последующее дифференцирование уменьшает число значащих цифр на 1 [6, Operators-Calculus operators-nth derivative].

Возможности вычисления зависимости производной от переменных и параметров (для рядного или векторного представления) практически аналогичны вычислениям по формуле (см. поз.1).

6. Интегрирование

Время вычисления интеграла с функциями Бесселя (первого рода порядков 2…9 и модифицированной функции первого рода 2–го порядка) и экспонентой  из (1.4) с построением таблицы расчета в 1280 строк зависимости интеграла от параметров a, c, m и b  – 89 с (рис.1.4).