Санкт-Петербургский Государственный Политехнический Университет
Факультет Технической Кибернетики
Кафедра Системного Анализа и Управления
Лабораторная работа №2
Курс: «Теория автоматического управления»
Тема: «Разработка и исследование линейных непрерывных систем с модальным регулятором»
Выполнил: ст. гр. 3082/2
Дегтярёв И.В.
Проверил: проф. каф. САиУ
Куприянов В. Е.
Санкт-Петербург
2007
1. Цели работы
1. Знакомство с методикой синтеза модальных регуляторов.
2. Исследование разработанной системы управления с использованием среды визуального моделирования Simulink пакета MatLab.
2. Ход работы
2.1. Расчет параметров регулятора.
Синтез модального регулятора проводится для объекта, заданного математической моделью в пространстве состояний
![]()
с параметрами  ,
, 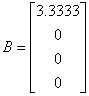 ,
,
![]() ,
, ![]() .
.
Собственные значения исходной матрицы, определяемые в среде MatLab:
>> Lam=eig(A)
Lam =
-4.5507
-1.0520
-0.7257 + 0.5344i
-0.7257 - 0.5344i
Коэффициенты характеристического уравнения, соответствующие компонентам вектора Lam:
>> p=poly(Lam)
p =
1.0000 7.0542 13.7319 11.5000 3.8889
Т.к. ![]() ,
а
,
а ![]() , то вектор
, то вектор ![]() ,
составленный из компонентов p:
,
составленный из компонентов p:
>> a=[p(5); p(4); p(3); p(2)]
a =
3.8889
11.5000
13.7319
7.0542
Для приведения модели системы к
канонической форме вычисляются матрицы ![]() :
:
>> S=ctrb(A,B); T=[p(4) p(3) p(2) 1; p(3) p(2) 1 0; p(2) 1 0 0; 1 0 0 0]; Q=S*T
Q =
0.4167 4.4305 12.4027 3.3333
0.4167 4.3055 11.1110 0
0.4167 3.0555 4.4444 0
0.2778 0.5556 0 0
Для проверки правильности
проделанных вычислений убедимся в соответствии преобразованной системы
канонической форме ![]() :
:
>> Af=inv(Q)*A*Q
Af =
-0.0000 1.0000 0.0000 0.0000
-0.0000 0.0000 1.0000 -0.0000
0.0000 -0.0000 0.0000 1.0000
-3.8889 -11.5000 -13.7319 -7.0542
>> en= inv(Q)*B
en =
-0.0000
0.0000
-0.0000
1.0000
Зададим требуемые собственные значения для
характеристического полинома системы. Нам необходимо создать устойчивую
систему, а значит, действительные части этих значений должны быть меньше 0: ![]() . Для заданных собственных значений
время переходного процесса равно:
. Для заданных собственных значений
время переходного процесса равно: ![]() . Тогда вектор
. Тогда вектор ![]() , соответствующий вектору
, соответствующий вектору ![]() , определяется следующими
вычислениями:
, определяется следующими
вычислениями:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.