Разработка и исследование линейных непрерывных систем с модальным регулятором, страница 2

>> Lu=[-4.5; -1.0; -0.2; -1.2];p=poly(Lu);pu=[p(5); p(4); p(3); p(2)]

pu =

    1.0800

    7.6200

   12.4400

    6.9000

Параметры модального регулятора, задаются вектором k:

>> k=inv(Q')*(a-pu)

k =

    0.0463

    1.0864

   -2.5544

   12.2447

Матрица замкнутой системы  :

>> Az=A+B*k'

Az =

   -3.1792    3.6213   -8.5145   -0.8514

    3.3333   -3.3333         0         0

    1.3333   -1.1333   -0.2000         0

         0         0    0.1250   -0.1875

Для обеспечения заданного значения управляемой переменной найдем величину необходимого коэффициента усиления  :

>> ku=1/(C*inv(-Az)*B)

ku =

    3.8880

Проделанные вычисления позволяют реализовать моделирование процессов в среде Simulink.

2.2. Исследование линейной непрерывной системы с модальным регулятором

На рис.1 представлена блок-схема моделируемой системы.

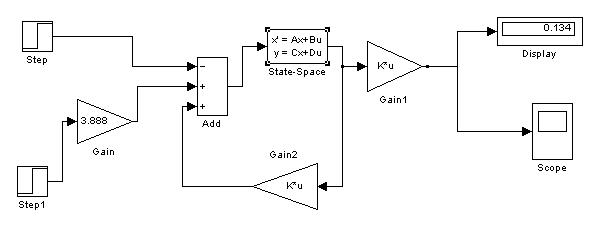
Рис. 1

Блок Space соответствует объекту управления, однако, предполагает некоторую особенность задаваемых параметров блока. В связи с тем, что стабилизация системы осуществляется в функции от вектора состояния и выходной сигнал этого блока равен , параметры C и D задаются как . Блок  Gain 1 предназначен для формирования управляемой переменной , что приводит к заданию параметров блока . Блок  Gain2, включенный в цепь обратной связи, должен иметь параметры, определенные как параметры регулятора . Блок  Step 1 предназначен для формирования заданного значения управляемой переменной. Усилитель Gain реализует коэффициент передачи  . Step отражает подачу нагрузки (возмущение) на систему.

1. Отработка ненулевых начальных условий.

Необходимо выбрать для вектора  такое значение, чтобы оно соответствовало постоянной величине управляемой переменной . Величина уставки и возмущения нулевые: , .

Поскольку в данной модели четвертая компонента вектора совпадает с управляемой переменной, то задаем . График процесса,  полученный при исследовании заданной модели, представлен на рис. 2.

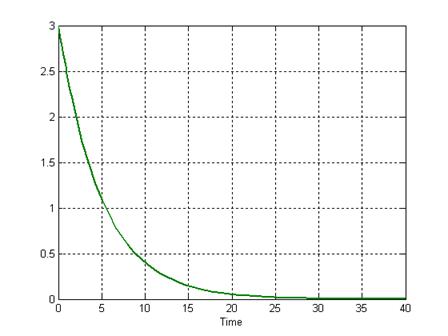
Рис. 2

Сравним этот график с результатом функции initial пакета MatLab, представленном на рис. 3.

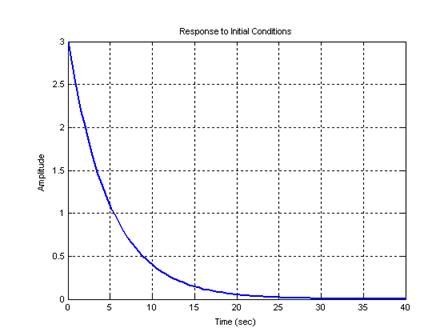
Рис. 3

Очевидно, что графики на рис. 2 и 3 совпадают.

2. Ступенчатое изменение уставки

Исследуем модель со следующими свойствами: , ,  .

График исследуемого процесса представлен на рис. 4

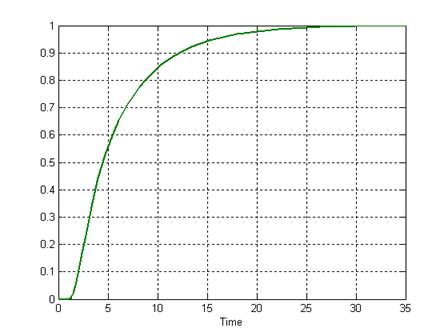
Рис. 4

График этого же процесса, полученный при помощи функции step, представлен на рис. 5.

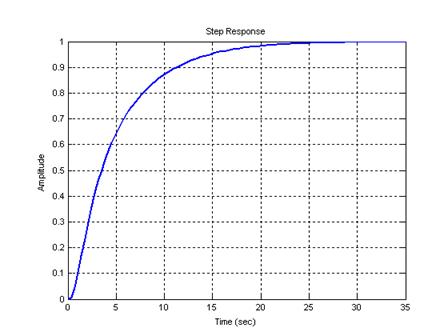
Рис. 5