Исследование линейных цепей синусоидального тока (Лабораторная работа № 2), страница 4

Выражение в скобках это сумма двух сопротивлении: R- сопротивление резистора, а

jωL- комплекс индуктивного сопротивления. Обозначим: Z= R+jωL = |Z| e^jφ, где

- модуль (входного) сопротивления цепи, α= 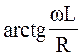- аргумент входного сопротивления. Уравнение (2.3) примет вид  ZI_m=E_m. Это закон Ома в комплексной (символической) форме. Выражая ток, получим:

I_m= = 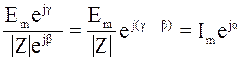,                             (2.4)

где:I_m- амплитудное значение тока, α-  фаза тока.

Зная комплекс тока, можно получить: i(t)=I_msin(ωt+α). Основной расчет закончен.

В цепях переменного тока широко используют понятие действующего значения.

Для синусоидального тока действующее значение: I=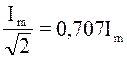

На практике, при расчете цепей символическим методом, дифференциальное уравнение вида (2.2) обычно не составляют. А составляют, используя принципы символического метода, расчетную схему. Исходной схеме (рис.2.2) соответствует расчетная схема (рис.2.5).                                     Принято обозначать:

                      U_R                                  Е=- комплекс действующего значения э.д.с;

jX_L=jωL-комплекс индуктивного сопротивления;

U_R = IR- комплекс напряжения на резисторе;

EjX_LU_L           U_L =IjX_L- комплекс напряжения на индуктивности.

Главное отличие расчетной схемы от исходной в в том, что она содержит только сопротивления и источники э.д.с.(и/или источники тока). В этом смРис.2.5.Расчетная схема               ысле нет никакой разницы между цепями постоянного тока и цепями синусоидального тока. Но при расчете цепей постоянного тока мы имеем дело с алгебраической системой уравнении с вещественными коэффициент- ами, а цепях синусоидального тока , применяя символический метод, получаем также алгебраическую систему уравнении, с комплексными  коэффициентами. В том и другом случае, систему уравнении получают, используя законы Кирхгофа, которые к тому же лежат в основе главных методов расчета: контурных токов и узловых потенциалов. Следовательно, указанные методы можно применять для анализа расчетных схем, полученных с помощью символического метода.

Вернемся к расчетной схеме  и введем ряд важных понятии (таблица 2.5).

Таблица 2.5

	Понятие	Расчетное выражение	Пример
1	Сопряженный комплекс тока		I=10ej30;  =10e-j30
2	Комплекс полной ( кажущейся) мощности	РК-активная мощность QK-реактивная мощность	ЕГЕН=560○   IГЕН=2-15○ =  2,58+j9,65; PГЕН=2,58 Вт   QГЕН=9,65 BAp
3	Баланс полной мощности		РНАГ=РГЕН QГЕН= QНАГ
4	Реактивное сопротивление	XL=2πfL=ωL (индуктивное) XC=(емкостное)	L=0,1Гн ω=100 XL=10 Ом С=10 мкФ ХС=103 Ом

Обратим особое внимание на векторные диаграммы, которые позволяют более отчетливо понять процессы, имеющие место в схеме. Векторные диаграммы бывают двух типов: количественные и качественные. Первые строятся по результатам расчета. Вторые, на теоретической  основе, с качественным применением законов Кирхгофа и закона Ома в символической форме.  

Построим качественную векторную диаграмму для схемы по рис.2.5.Построение  проведем для действующих значении комплексов тока и напряжении, используя ура-          внение (2.3). Построение проводят на комплексной плоскости (рис.2.6). Рекомендуем придерживаться следующего порядка: 1.Проводим оси комплексной плоскости (1, J)

2.Выбираем вектор c которого начинаем постр                       J                                             ение. При последовательном соединении соп-       

U_L                  ротивлении надо начинать с вектора тока- I.

3.Строим вектор напряжения на сопротивлении

UR

                                                                R- U_R=IR. Он совпадает с вектором токаI.