Таблица 2.10
|
ток |
напряжение на резисторе |
напряжение на емкости |
|
i(t)=I |
uR(t)=RI |
uC(t)= |
Качественную векторную диаграмму для этой цепи, авторы надеются, Вы по- строите сами. Расчет активной мощности в цепи R-C не отличается от расчета в цепи R-L. Реактивная мощность генератора рассчитывается по выражению: QГЕН=ЕIsinφ.
Реактивная мощность нагрузки ( в емкости ) равна:QНАГ=-I2XC. Естественно, что должен выполнятся баланс мощностей: QГЕН= QНАГ.
Б.Расчетная подготовка к проведению эксперимента
Исходные данные и задание для подготовки к выполнению лабораторной работы приведены в (таб.2.6), расчет цепи R-C.
В. Сборка схемы.
В собранной Вами схеме R-L (рис.2.7), уберите L и поставьте C (емкость). Она находиться на той же панели, где и индуктивнось (рис.2.9), слева. Поставьте величину емкости и приступайте к эксперименту.
Г.Экспериментальный и расчетный анализ.
Анализ проведем используя нижеприведенную таб. 2.11
|
ЭКСПЕРИМЕНТ |
РАСЧЕТ |
|||||||||
|
f |
A |
W |
ω |
cosφ |
φ |
|
XР |
I |
UР |
Q |
|
Гц |
A |
Bт |
1/C |
- |
○ |
Oм |
Oм |
A |
B |
BAр |
|
0,2f0 |
||||||||||
|
0,5f0 |
||||||||||
|
0,8f0 |
||||||||||
|
f0 |
||||||||||
|
1,2f0 |
||||||||||
Эксперимент начните с частоты генератора f=f0. Снимите показания амперметра (А) и ваттметра (W), затем проведите расчет этого режима (ω, cosφ и.т.д) и сравните полученные результаты с теми, которые Вы получили про подготовке к лаб. работе (смотри результаты в таблице 2.6). При хорошем совпадении проведите остальные опыты и приступайте к построению графиков. В противном случае, разберитесь в чем дело, сами или с преподавателем. Примечание: ХР, UР- соответственно индуктивное сопротивление и напряжение на емкостном сопротивлении.
Д. Построение графиков и анализ результатов моделирования.
Припостроении использовать
относительную частоту: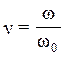 
.
Произвести построение
зависимостей аналогичных, рассмотренным в (таб. 2.8). Естественно, что необходимо
определить Iмах, Рмах,
Qмах и
значения частот на которых они наблюдаются. Для этих
исследовании рекомендуем ввести константу: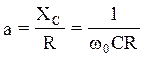
;
Координатные оси, аналогичны осям на рис.2.11÷2.13. Заполните таблицу 2.12.
Таблица 2.12
|
|
|
|
|
|
|
|
Примечание: Вопросы для зачета по 2ой схеме в конце 2ой лабораторной работы.
Приступим к выполнению пункта №3:
3. РЕЗОНАНС В ПОСЛЕДОВАТЕЛЬНОЙ ЦЕПИ R-L-C.
A.Теоретические сведения.
Рассмотренные выше цепи R-L и R-C, несмотря на их простоту, позволяют часто, описать ход процессов во многих электротехнических устройствах. Но сложность устройств растет, возрастают требования к точности и адекватности соответствия расчетных моделей (цепей ) и реальных объектов моделирования.
|
Это приводит
к необходимости рассмотрения все более сложных по структуре (числу узлов, ветвей)
и виду элементов (кроме R,L,C имеется масса новых) электри- ческих
цепей. В данной работе рассмотрим простую по структуре цепь, состоящую из
последовательно соединенных резистора, индуктивности и емкости, подключенных к
синусоидальному источнику э.д.с. В схеме один контур, следовательно, можно запис
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
Z
=
=
=f4(ν)=
=f5(ν)=
=f6(ν)=