Исследование линейных цепей синусоидального тока (Лабораторная работа № 2), страница 3

    Примечание:   (    =НАЖАТЬ ).                                                           

Таблица 2.4

Продолжение таблицы 2.4

Главное свойство комплексной плоскости связано с синусоидальной функцией. Представьте себе, что вектор С вращается с угловой скоростью - ω против часовой стрелки. В таком случае, угол между вектором и осью абсцисс будет меняться  по закону φ_t=φ+ωt, где φ-начальное значение (см. рис.2.4). Проекция вектора на ось J будет равна b= Csinφ_t= Csin(φ+ωt)= Csin(ωt+φ), т.е будет являться синусоидальной функцией времени. Следовательно, вместо того, чтобы оперировать с самой синусоидальной функцией, можно использовать вектор С, который соответствует ей на комплексной плоскости. Соответствие показывают следующим образом :(Се^jφе^jωt)~

Csin(ωt + φ). Равенство имеет вид: Csin(ωt + φ)= Im(Се^jφе^jωt).

Пусть имеются две синусоидальные функции: C₁sin(ωt + φ₁) и C₂sin(ωt + φ₂). У них разные амплитуды(C₁, C₂), начальные фазы(φ₁, φ₂) , но одна и та же угловая скорость ω. Каждой функции можно поставить в соответствие на комплексной плоскости свой вектор. Они вращаются с одной и той же угловой скорость  ω, следовательно относительно друг друга они неподвижны. Eсли найти, например, сумму этих векторов, то результирующий вектор будет соответствовать третьей синусоидальной функции: C₃sin(ωt + φ₃)= C₁sin(ωt + φ₁)+ C₂sin(ωt + φ₂).

Тогда, можно сделать важный вывод. Если в электрической цепи, все токи и напряжения являются синусоидальными функциями времени, то действия над этими функциями можно заменить действиями на комплексной плоскости с векторами соответствующих синусоидальным функциям. В этом суть символического метода.

Вернемся к уравнению (2.2). Итак, если нас интересует только установившийся режим, то, как следует из рис.2.3, при t ≥ 5мС и э.д.с. и ток являются синусоидаль- ными функциями времени. Поэтому, э.д.с. е(t)= E_msin(ωt +γ) поставим в соответствие комплекс E_m =Е_me^jγ , а рассчитываемому току i(t) комплекс I_m=I_me^jα. В уравнении (2.2) присутствует производная тока. Мы не знаем ни амплитуды тока (I_m), ни начальной фазы (α), но мы знаем, что ток i(t)= I_msin(ωt+α). Производная тока по времени равна: 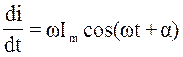=ωI_msin(ωt+α+90^○). Эта функция отличается от функции тока множителем ω и начальной фазой 90^○. Поэтому ей на комплексной плоскости будет соответствовать вектор, длина которого в ω раз больше длины вектора тока и который повернут относительно последнего на угол 90^○. Учитывая это, можно записать:ωI_msin(ωt+α+90^○)~ωI_me^jαe^j90. По формуле Эйлера:e^j90= сos90^○+jsin90^○ = j

Таким образом:~ jωI_me^jα=jωI_m. А уравнению (2.2) будет соответствовать уравнение

                                             I_mR+ jωLI_m= E_m                                                                                               (2.3)                                                                             

Решение уравнения не является проблемой. Вынося I_m, получим:I_m(R+jωL)=E_m.