





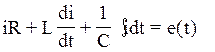


Это дифференциальное уравнение 2-ого порядка.
Решение уравнения
позволяет найти закон изме

нения
тока и любого напряжения с момента вре

мени
t=0, т.е. с момента включения э.д.с.
На
рис.2.18 показаны графики тока (тонкая линия)

и напряжения на
емкости. Внимательно рассмотрРис.2.17 Расчетная схема ите
этот рисунок. Начнем с t=0. Значение э.д.с. е(0) равно
10
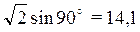
.Это амплитудное (максимальное) значение напряжения,
которое может создать источник. Ток- i(0)=0, напряжение на емкости- u
C(0)=0. Это соответствует законам коммутации, с которыми Вы по- знакомитесь позже. Но смотрите,
что происходит дальше. Время увеличивается, увеличиваются ток и напряжение
на емкости. Это нормально. Очень интересно другое:
максимальное напряжение на
емкости с момента времени t≥10 миллисекунд становиться больше амплитудного
значения э.д.с. равного 14,1 В и продолжает расти.
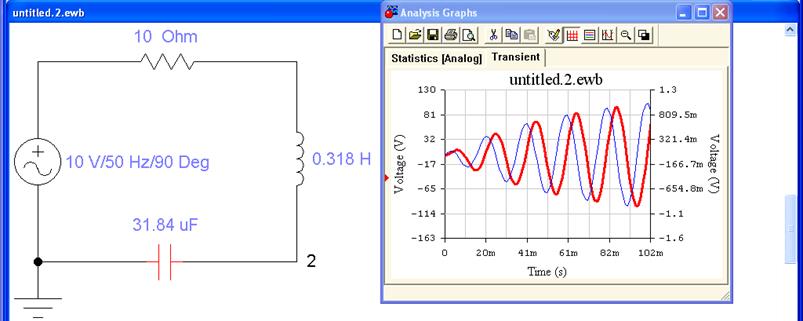
 Рис. 2.19 Графики тока и напряжения на емкости в
переходном процессе в цепи RLC.
Рис. 2.19 Графики тока и напряжения на емкости в
переходном процессе в цепи RLC.
Когда переходный процесс закончиться, под действием синусоидальной
э.д.с, ток и все напряжения будут тоже меняться по синусоидальному закону.
Учитывая характер
изменения напряжения на емкости представляет большой интерес максималь
ное значение этого напряжения и как его
рассчитать.

Воспользуемся
символическим методом. Расчетная схема





 приведена на
рис.2.20. Так как в схеме один источник, то
приведена на
рис.2.20. Так как в схеме один источник, то


то
проще всего провести расчет, используя комплекс вхо

дного
сопротивления:
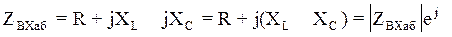
(2.8)


Рис.2.20. Расчетная
схема
|
|


где:
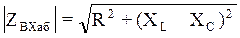
- модуль сопротивления,
φ = аrctg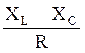 - аргумент входного сопротивления.
- аргумент входного сопротивления.
Пусть параметры R,L,C величины постоянные, а меняется
только частота генератора-f. В этом случае, в схеме будут меняться прежде всего
сопротивления XL=2πfL и XC=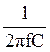 и на какой-то частоте f0 эти сопротивления будут равны.
и на какой-то частоте f0 эти сопротивления будут равны.
Найдем f0: 2πf0L =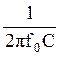 ; f0=
; f0=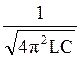 или
или 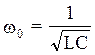 (2.9)
(2.9)
На этой частоте XL-XC=0, 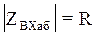 - имеет минимальное значение и чисто
активное, а аргумент φ=0. Это значение частоты, получило название резонансной
для последоввательной цепи RLC. На резонансной частоте по закону Ома ток:
- имеет минимальное значение и чисто
активное, а аргумент φ=0. Это значение частоты, получило название резонансной
для последоввательной цепи RLC. На резонансной частоте по закону Ома ток: 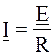 и совпадает по фазе с э.д.с. Для всех остальных
частот входное сопротивление является комплексной величиной, зависящей от
частоты. Следовательно от частоты зависит ток в цепи, который определяется по
закону Ома в комплексной форме:
и совпадает по фазе с э.д.с. Для всех остальных
частот входное сопротивление является комплексной величиной, зависящей от
частоты. Следовательно от частоты зависит ток в цепи, который определяется по
закону Ома в комплексной форме: 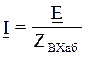 , а также напряжение на
любом сопротивлении в схеме. Зависимости сопротивлении, токов, напряжении от
частоты получили название частотных зависимостей. В таблице 2.13
приведены выражения частотных зависимостей с использованием важ- ной
характеристики- добротности контура:
, а также напряжение на
любом сопротивлении в схеме. Зависимости сопротивлении, токов, напряжении от
частоты получили название частотных зависимостей. В таблице 2.13
приведены выражения частотных зависимостей с использованием важ- ной
характеристики- добротности контура: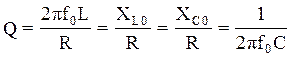 (2.10)
(2.10)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
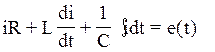
![]()

![]() Рис. 2.19 Графики тока и напряжения на емкости в
переходном процессе в цепи RLC.
Рис. 2.19 Графики тока и напряжения на емкости в
переходном процессе в цепи RLC.![]()
![]()
![]()
![]()
![]()
![]()
![]() приведена на
рис.2.20. Так как в схеме один источник, то
приведена на
рис.2.20. Так как в схеме один источник, то ![]()
![]()
![]()
![]()
![]()
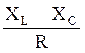 - аргумент входного сопротивления.
- аргумент входного сопротивления.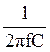 и на какой-то частоте f0 эти сопротивления будут равны.
и на какой-то частоте f0 эти сопротивления будут равны.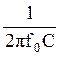 ; f0=
; f0=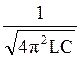 или
или 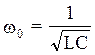 (2.9)
(2.9)![]() - имеет минимальное значение и чисто
активное, а аргумент φ=0. Это значение частоты, получило название резонансной
для последоввательной цепи RLC. На резонансной частоте по закону Ома ток:
- имеет минимальное значение и чисто
активное, а аргумент φ=0. Это значение частоты, получило название резонансной
для последоввательной цепи RLC. На резонансной частоте по закону Ома ток: 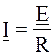 и совпадает по фазе с э.д.с. Для всех остальных
частот входное сопротивление является комплексной величиной, зависящей от
частоты. Следовательно от частоты зависит ток в цепи, который определяется по
закону Ома в комплексной форме:
и совпадает по фазе с э.д.с. Для всех остальных
частот входное сопротивление является комплексной величиной, зависящей от
частоты. Следовательно от частоты зависит ток в цепи, который определяется по
закону Ома в комплексной форме: 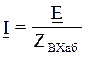 , а также напряжение на
любом сопротивлении в схеме. Зависимости сопротивлении, токов, напряжении от
частоты получили название частотных зависимостей. В таблице 2.13
приведены выражения частотных зависимостей с использованием важ- ной
характеристики- добротности контура:
, а также напряжение на
любом сопротивлении в схеме. Зависимости сопротивлении, токов, напряжении от
частоты получили название частотных зависимостей. В таблице 2.13
приведены выражения частотных зависимостей с использованием важ- ной
характеристики- добротности контура: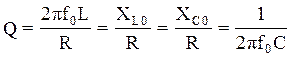 (2.10)
(2.10)