Методы планирования эксперимента, страница 6

Пусть требуется исследовать 6 факторов X₁…X₆ и с помощью ПСБ выделить самые существенные.

1.1.            Разбиваем 6 факторов на 2 равные группы;

  1.2.            Для обеих групп cтроим ПФП 2³;

  1.3.-1.4.     Смешиваем строки и стыкуем планы для обеих групп.

В результате получаем ПСБ, представленный в таблице.

Таблица.

      ПФП 2³ 1-ой группы                               ПФП 2³ 2-ой группы

       (после смешивания)                              (после смешивания)

II.         Проведение эксперимента согласно матрице ПСБ и нахождение значения отклика y.

III.       Выделение существенных переменных

III.1.    Построение диаграммы рассеяния.

III.1.1. Для каждого фактора проводится своя ордината (рисунок), на которой точками    отмечают значения отклика у (берут из таблицы), причем слева отмечают у, соответствующий нижнему уровню фактора (-1), а справа – верхнему (+1).

III.1.2. Слева и справа от ординаты находят частные медианы. Медиана – такое значение случайной величины у, по обе стороны от которой лежат равные количества точек измерения у, независимо от их значений.  

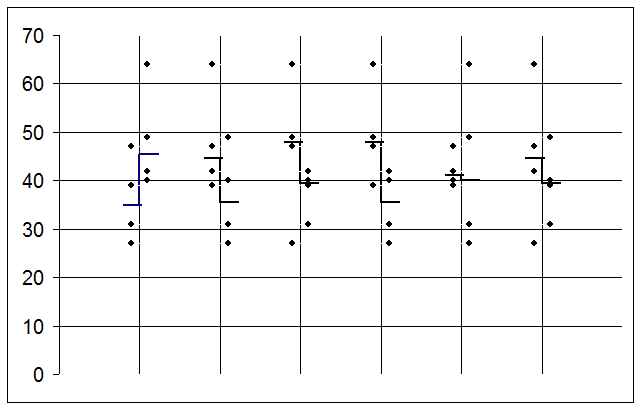
III.1.3. Определяется вклад каждого фактора х_i в целевую функцию у, который обозначается как Вх_i и рассчитывается как разность между медианой справа и медианой слева. Из рисунка, построенного по данным таблицы видно, что

Вх₁= 45,5 – 35 = 10,5;            Bx₄= 35,5 – 48 = -12,5;

Bx₂= 35,5 - 44,5 = -9;             Bx₅= 40 – 41 = -1;

Bx₃= 39,5 – 48 = -8,5;                        Bx₆= 39,5 - 44,5 = -5.

III.1.4. Для каждого фактора определяется количество “выделяющихся точек”, т.e. количество  точек, характеризующих сдвиг уровня  +1 относительно уровня -1. Например, для фактора х₁ сдвиг характеризуется двумя точками сверху и тремя снизу (5 точек).

III.1.5. Производится выделение наиболее существенных факторов (все факторы укладываются в ряд по значимости) исходя из (1) численных значений вкладов Вх_i и (2) количества “выделяющихся точек”. Для описываемого случая это х₄ и х_1.

III.1.6. Исключение влияния наиболее существенного фактора методом “стабилизации”. Стабилизация х₄ на уровне -1осуществляется вычитанием вклада Вх₄ со своим знаком из величины у в тех столбцах, где уровень х₄= +1:

у^I= у - Вх_i,

где у - исходное значение отклика,  у^I - значение отклика после первой корректировки.

Значение у на другом уровне варьирования (х₄= -1) остается при этом неизменным.

III.1.7. По данным у^I строят новую диаграмму рассеяния и процедуру повторяют, определяя следующую по рангу влияния переменную, имеющую наибольший вклад и т.д.