Методы планирования эксперимента, страница 5

Разрешающая способность реплики определяется порядком взаимодействия, входящего в генерирующее соотношение. Чем выше порядок взаимодействия, тем выше разрешающая способность реплики. Так, разрешающая способность тройных эффектов взаимодействия факторов выше чем парных, четверных – выше чем тройных и т.д.Поэтому в случае построения ДФП 2^4-1 выбирается генерирующее соотношение Х₄=Х₁Х₂Х₃.

Однако приравнивание фактора к взаимодействию имеет следствием не только существенное сокращение числа опытов ДФП по сравнению с ПФП, но также приводит к изменению системы оценок коэффициентов математической модели. Применение ДФП неизбежно связано со смешиванием, т.е. совместным оцениванием нескольких коэффициентов регрессии. Чтобы показать как это происходит дадим характеристику определяющего контраста.

Определяющий контраст (ОК) получается в результате умножения обеих частей генерирующего соотношения на его левую часть (эффект фактора) и всегда равен единице (т.к. любое Х_i²=+1). Для выше рассмотренного примера построения ДФП 2^4-1 определяющим контрастом будет произведение Х₁Х₂Х₃Х₄.

Проведя последовательное умножение ОК на все х_i в матрице плана и, имея в виду, что вектор х_i² содержит только +1, получим:

х₁=х₂х₃х₄; х₂=х₁х₃х₄; х₃=х₁х₂х₄; х₄=х₁х₂х₃

Эти соотношения указывают на равенство определённых вектор-столбцов в матрице плана, что приводит к получению смешанных оценок коэффициентов модели, рассчитанных с их помощью:

в₁→β₁+β₂₃₄; в₂→β₂+β₁₃₄; в₃→β₃+β₁₂₄; в₄→β₄+β₁₂₃,

где в_i – выборочная оценка i-го коэффициента регрессии;

       β_i – его истинное значение.

Вероятность искажения оценок из-за эффекта смешивания обуславливает ограничения использования ДФП.

В каких случаях используется ДФП?

(1) Если  априори можно принять, что влияние взаимодействий (произведений факторов) второго и высших порядков (как х₁х₂, х₁х₃, х₁х₂х₃ и т.д.)  отсутствует или пренебрежимо мало.

(2) На первых этапах исследования, когда нужно получить в первом приближении лишь линейную аппроксимацию изучаемой зависимости.

(3) Когда большое количество опытов ПФП при большом количестве факторов экономически не целесообразно.

Основное достоинство ДФП: сохранение свойств ортогональности плана при одновременном уменьшении количества опытов.

2.1.3.   План случайного баланса (ПСБ)

Насыщенность плана - это соотношению количества опытов N и числа факторов к

По насыщенности все планы можно разделить на:

(1) ненасыщенные, когда k < N-1 (ПФП, часть ДФП);

(2) насыщенные, когда k = N-1 (часть ДФП);

(3) пересыщенные, когда k >N-1 (ПСБ).

Планом случайного баланса (ПСБ) называется план, реализующий случайную выборку ПФП или ДФП таким образом, что количество опытов N в матрице плана меньше, чем число факторов k + 1:

N < k +1

Т.о,  ПСБ является перенасыщенным планом.

При условии перенасыщенности невозможно получить независимые количественные оценки коэффициентов уравнения регрессии для всех рассматриваемых переменных. Поэтому задача ПСБ состоит в выделении существенных переменных и отнесении всех несущественных или малосущественных переменных к «шумовому полю». Если число существенных переменных h подчиняется условию:

h < N-1,

то они (существенные переменные) могут быть оценены независимо, в результате расщепления математической модели на части.

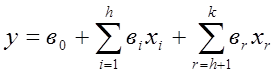
где       k – общее число переменных (факторов);

h – число значимых переменных;

k-h – число незначимых переменных.

ПСБ применяется при соблюдении условий:

(1)  При изучении более 8-10 факторов, когда применение ПФП и ДФП оказывается слишком громоздким для постановки отсеивающих опытов.

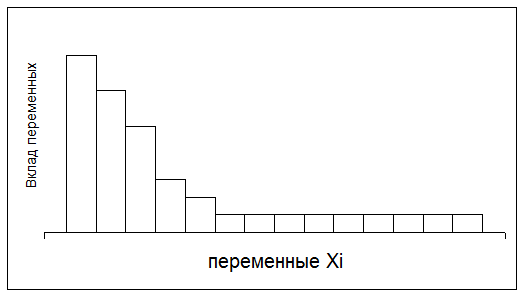
(2)  Если заведомо известно, что лишь немногие переменные (10-15%) являются действительно существенными, а остальные могут быть отнесены к «шумовому полю». Постулируется, что для успешного применения ПСБ переменные, расположенные в порядке убывания вкладов, вносимых ими в общую дисперсию отклика, должны образовывать быстро затухающую кривую (рисунок).

Схема (последовательность) работы ПСБ

I.          Построение матрицы ПСБ:

1.1.  все факторы, смешанные случайным образом, разбивают на группы;

1.2.  для каждой группы составляют МП (матрицу плана) на основе ПФП или ДФП;

1.3.  все строки МП для каждой группы смешивают случайным образом;

1.4.  МП каждой группы стыкуют в один ПСБ.

Построение ПСБ рассмотрим на примере.