Методы планирования эксперимента, страница 3

номер	факторы
X0+J1   X0   опыта	x1	x2
X0 - J1   X1   1	1	1
2	-1	1
3	1	-1
X0 - J2   4(-1,-1)   3(+1,-1)   4	-1	-1

В случае двух факторов все возможные комбинации их уровней можно найти прямым перебором, но с ростом числа факторов необходимо знание приемов построения матрицы плана.

Существует два основных приема построения МП:

Таблица 4 иллюстрирует оба описанных ниже приема

                                                Таблица 4

(1)  При добавлении каждого нового фактора для прежних факторов исходный план дублируется, а для вводимого фактора его верхний и нижний уровень (в кодированном выражении +1 и -1) записывают в одинаковых количествах.

(2)  Прием основан на правиле чередования знаков. В первом столбце матрицы знаки меняются поочередно, во втором – чередуются через 2, в третьем – через 4, в n-ом – через 2ⁿ.

Свойства ПФП 2^k

(1) Симметричность относительно центра эксперимента. Это свойство следует из правила построения МП и может быть записано: Алгебраическая сумма элементов каждого вектор-столбца матрицы равна нулю:

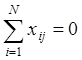
где Xij – уровень j-го фактора в i-м опыте

(2) Условие нормировки: Сумма квадратов элементов каждого столбца равна числу опытов

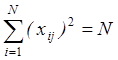
Это свойство следует из того, что уровни факторов в МП задаются +1 и -1

(3) Ортогональность: Сумма скалярных произведений всех вектор-столбцов равна нулю:

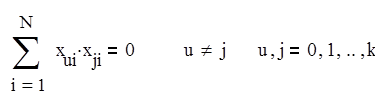
(4) Ротатабельность: свойство, означающее независимость точности предсказания значений отклика от расстояния от центра плана.

Полный факторный план позволяет количественно оценивать не только эффект каждого фактора, но и эффект взаимодействия факторов. Для этого в МП добавляют вектор-столбцы двойного, тройного, и так далее взаимодействия, которые получают перемножением столбцов соответствующих факторов (см. таблицу); при этом число опытов не изменяется.

Т. О. векторные столбцы  x₁, x₂, x₃ определяют условие эксперимента, а x₀, x₁x₂, x₂x₃, x₁x₂x₃ – служат только для расчета коэффициентов b₀, b₁₂, b₂₃, b₁₂₃ в уравнении регрессии.

2.1.2  Дробный факторный план (ДФП)

ДФП – план реализующий часть (дробную реплику) ПФП (1/2, 1/4, и т д)

Для ДФП число опытов N рассчитывают по формуле:

N = p ^k-l

где       р – число уровней варьирования фактора

k – общее число факторов

l- число линейных эффектов, приравненных к эффектам взаимодействия

k-l – число факторов в ПФП, к которому приравнивается дробная реплика.

Если число уровней каждого фактора равно двум то тип дробной реплики обозначается как 2^k-l

Рассмотрим принцип построения ДФП из ПФП на примере ПФП типа 2³ (число факторов k=3,число уровней каждого фактора р=2).Условием (предпосылкой) для возможности создания ДФП из ПФП является факт, что при добавлении к матрице ПФП столбцов, отражающих эффекты взаимодействия факторов, все свойства ПФП сохраняются.