Математика \ Теория вероятностей и математическая статистика

Статистическая оценка неизвестных параметров распределения, страница 6

Построение доверительного интервала для МО СВ, имеющей нормальное распределение с известным СКО

Пусть  x~N(M[x], s[x]), причём s[x] – известно, а  M[x]=?.

1. Определяется точечная оценка МО по выборке объема   n

.

Поскольку 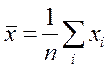 , где xi – значения одной и той же СВ x, то в силу центральной предельной теоремы, ~N(M[],s[]).

Поскольку точечная оценка  является несмещенной, то . СКО оценки  МО СВ x равно

.

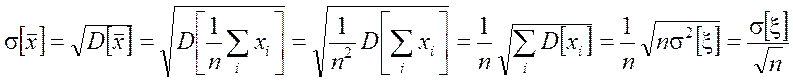2. Рассмотрим вспомогательную случайную величину:

,

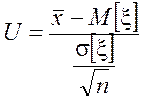которая, как и величина  имеет нормальное распределение с МО:

и дисперсией:

.

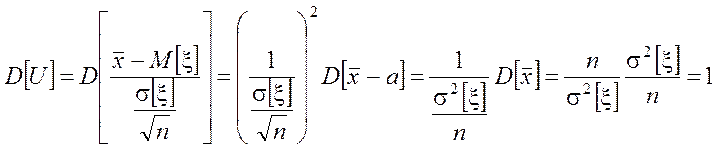Таким образом,  x~N(M[x],s[x]) ,  ~N (M[x],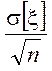) , а U~N(0;1).

3. Для заданной Pдов=1–a определяется интервал (,) из условий:

P{U<}=a/2; P{U>}=a/2.
 

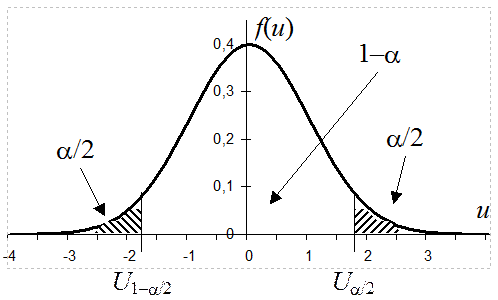
На основании симметрии функции плотности нормального распределения Ua/2=–U1-a/2. Квантили U уровня (1–a/2) и (a/2) определяются по таблицам квантилей стандартного нормального распределения.

4. Определив интервал (,), который с доверительной вероятностью накрывает значение U, определяется доверительный интервал для M[x] обратным преобразованием:

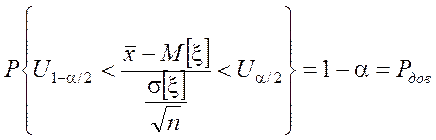 Þ  Þ
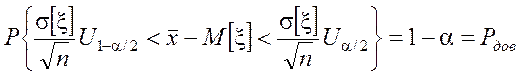Þ  Þ
Þ .

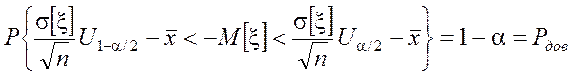Учитывая, что Ua/2=–U1-a/2

.

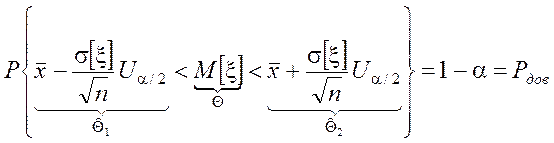Доверительный интервал найден. Абсолютная погрешность интервальной оценки МО равна: .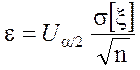

Построение доверительного интервала для МО СВ, имеющей нормальное распределение с неизвестным СКО

Пусть  x~N(M[x], s[x]), причём  M[x]=?, s[x]=?.

1. Определяется точечная оценка МО и СКО по выборке объёма n:

, .

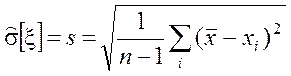2. Составляется вспомогательная СВ (выборочная статистика):

,

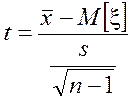которая имеет распределение Стьюдента с n=n–1 степенями свободы.

Таким образом, если  x~N(M[x], s[x]), то t~t(n–1).

3. Для заданной доверительной вероятности Pдов=1–a определяется интервал (t1–a/2, n–1, ta/2, n–1) из условий:

P{t < t1–a/2, n–1}=a/2;
P{t>ta/2, n–1}=a/2.
 

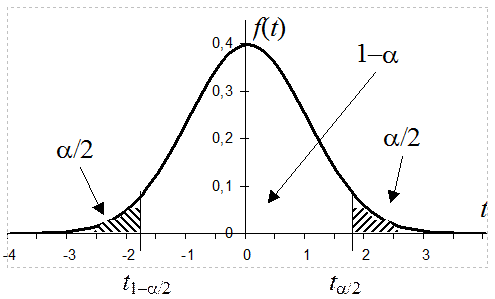
Квантили распределения Стьюдента уровня (1-a/2) и (a/2) для различного числа степеней свободы (n–1) определяются по таблицам. На основании симметрии функции плотности распределения Стьюдента  t1–a/2, n–1 = – ta/2, n–1 .

4. Определив интервал (t1–a/2, n–1, ta/2, n–1), который с доверительной вероятностью накрывает значение t, определяется доверительный интервал для M[x] следующим обратным преобразованием:

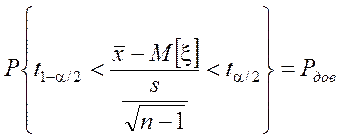 Þ

Þ  Þ
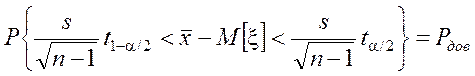Þ  Þ
Þ .

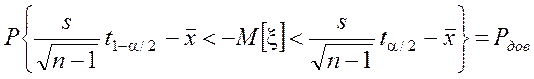Учитывая, что ta/2=–t1–a/2

.

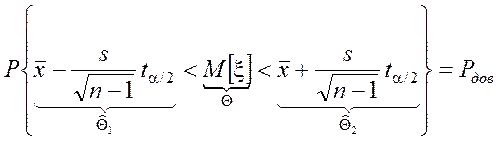Т.о. доверительный интервал для МО СВ, имеющей нормальное распределение с неизвестным СКО найден. Абсолютная погрешность оценки МО равна .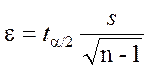

Построение доверительного интервала для СКО СВ, имеющей нормальное распределение

Пусть  x~N(M[x], s[x]), причём  M[x]=?, s[x]=?.

1. Определяется точечная оценка МО и СКО по выборке объёма n:

, .

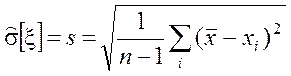2. Составляется вспомогательная СВ (выборочная статистика):

,

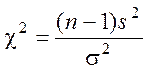которая имеет распределение c2   с n=n–1 степенями свободы.

Т.о., если  x~N(M[x], s[x]),  то c2 ~c2 (n–1).

3. Для заданной доверительной вероятности Pдов=1–a, определяется интервал (c2 1–a/2, n–1, c2 a/2, n–1) из условий:

P{c2  < c2 1–a/2, n–1}==a/2;

P{c2 > c2 a/2, n–1}==a/2.
 

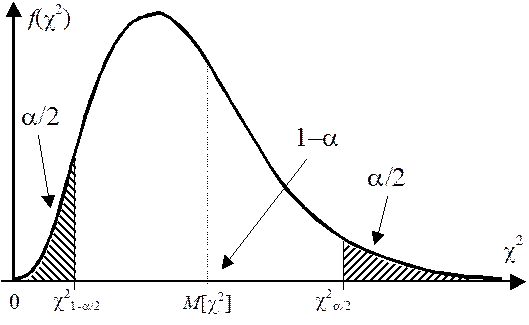
Квантили распределения c2  уровня (1–a/2) и (a/2) для различного числа степеней свободы (n–1) можно найти в специальных таблицах.

4. Определив интервал (c2 1–a/2, n–1, c2 a/2, n–1), который с доверительной вероятностью накрывает значение c2 , можно найти доверительный интервал для СКО s[x] следующим обратным преобразованием:

 Þ

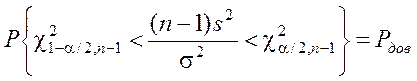Þ  Þ

Þ  .

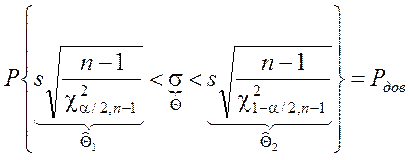Следовательно доверительный интервал для СКО СВ, имеющей нормальное распределение, найден.

Скачать файл