Статистическая оценка неизвестных параметров распределения, страница 2

Здесь снова следует подчеркнуть, что точечная оценка  параметра распределения  случайной величины x сама является случайной величиной, поскольку для различных выборок  будет принимать различные значения, заведомо неизвестные.

Сформулируем три основные требования к точечным оценкам числовых характеристик случайных величин.

Опр. Точечная оценка параметра =V(x₁, x₂,…x_n) называется состоятельной, если при увеличении числа испытаний оценка сходится по вероятности к значению оцениваемого параметра, т.е.

,

где e и d - произвольные положительные числа, близкие к нулю.

Это означает, что при увеличении объема выборки оценка скорее приближается к значению оцениваемого параметра, чем отдаляется от него.

Опр. Точечная оценка параметра =V(x₁, x₂,…x_n) называется несмещенной, если её математическое ожидание равно значению оцениваемого параметра, т.е.

.

Например, если оценивается дисперсия случайной величины D[x], то оценка дисперсии будет несмещенной если .

Иногда применяют асимптотически несмещенные оценки, для которых математическое ожидание оценки равно значению оцениваемого параметра при бесконечном увеличении объема выборки, т.е.

.

Состоятельные и несмещённые оценки могут быть получены различными способами. Например, математическое ожидание случайной величины x может быть оценено по формуле среднего арифметического элементов выборки () или как средний элемент вариационного ряда (). При этом каждая из оценок буден как состоятельной, так и несмещенной. Однако оценка , как случайная величина, имеет меньшую дисперсию (разброс значений) по сравнению с оценкой . Поэтому оценка  является более предпочтительной.

Опр. Точечная несмещенная оценка параметра =V(x₁, x₂,…x_n) называется эффективной, если она обладает минимальной дисперсией среди других возможных оценок исследуемого параметра.

Формулы для вычисления оценок некоторых числовых характеристик

Формулы для вычисления оценок основных числовых характеристик случайных величин представлены в [Математическая статистика: Лабораторный практикум/ Г. Ю. Мишин, Е. Л. Сазонова, Т. Т. Снопок, Д. Н. Шевченко; Под ред. В. С. Серёгиной. – Гомель: БелГУТ, 2001. , С. 7–8.]. В качестве оценки математического ожидания используется среднее арифметическое  элементов выборки. Для оценивания по выборочным данным моды распределения, используется то значение сгруппированного статистического ряда , которому соответствует наибольшее значение частоты. По интервальному статистическому ряду определяется модальный интервал, в который попало наибольшее число элементов выборки, и в качестве точечной оценки моды может использоваться середина этого интервала. В качестве оценки медианы  принимают средний (т. е. -й) член вариационного ряда, если значение n – нечётно, и среднее арифметическое между двумя средними (т. е. между -м и -м) членами этого ряда, если n – чётно.

Для несмещенной и состоятельной статистической оценки дисперсии используется статистика 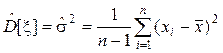. Оценка среднеквадратического отклонения: .

Оценка коэффициента вариации: .

Оценка коэффициента асимметрии :.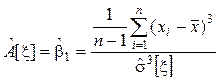

Оценка коэффициента эксцесса: .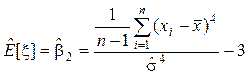

Докажем, что оценка математического ожидания, как среднее арифметическое элементов выборки, обладает свойством несмещённости и состоятельности.

Пусть x₁, x₂,…x_n – значения элементов выборки случайной величины x, которая имеет некоторое распределение F(x) с математическим ожиданием M[x]. Тогда значения элементов выборки можно рассматривать как n случайных величин, каждая их которых имеет распределение F(x) с математическим ожиданием M[x].