Статистическая оценка неизвестных параметров распределения, страница 3

Вычислим математическое ожидание оценки :

.

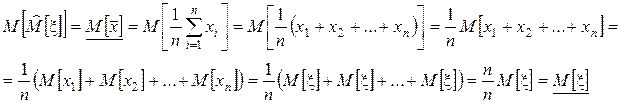Оно равно математическому ожиданию случайной величины x, таким образом, свойство несмещённости данной оценки доказано.

Доказательство свойства состоятельности оценки МО как среднего арифметического следует непосредственно из теоремы Чебышева, которую мы рассматривали в прошлом семестре: при достаточно большом числе независимых опытов среднее арифметическое наблюдаемых значений случайной величины x сходится по вероятности к её математическому ожиданию, т.е. , где 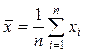 – среднее арифметическое наблюдаемых значений СВ x, а  e и d – произвольные сколь угодно малые положительные числа.

Таким образом, для СВ x, имеющей произвольный закон распределения, оценка МО как среднее арифметическое элементов выборки, является несмещенной и состоятельной. В некоторых случаях, в частности, если x~N(m,s) оценка  является ещё и эффективной (это без доказательства).

Интервальные оценки числовых характеристик случайных величин

Следует отметить, что свойства точечных оценок не ограничиваются несмещённостью, состоятельностью и эффективностью. Например, оценка вероятностей случайных событий по относительной частоте наступления СС в n испытаниях, является несмещенной и состоятельной, однако, например, при оценке вероятности безопасного функционирования в течение заданной наработки СЖАТ можно наблюдать ситуацию, что из 1000 устройств все проработали безопасно. В этом случае оценка ВБР равна единице, что все же не отвечает реальной действительности.

Кроме того, каковыми «хорошими» не были бы точечные оценки, в силу их случайности мы не можем знать на сколько отличается полученная оценка от реального значения оцениваемого параметра. Поэтому в ответственных исследованиях желательным является интервальное оценивание числовых характеристик и параметров распределения СВ.

Пусть найдена точечная оценка  числовой характеристики . Чем меньше разность |–|, тем лучше качество оценки, тем она точнее. Естественно, что точность оценки e зависит от n, но однозначной эта зависимость не является, можно говорить лишь о вероятности P_дов=(1–a) с которой точность оценки будет обеспечена, т.е. |–|<e.

Опр. Доверительной вероятностью оценки называется вероятность P_дов=(1–a) выполнения неравенства |–|<e. Если P_дов=0.95, то в 95% случаев при извлечении выборки и оценке некоторого параметра , его оценка  отклонится не более, чем на e.

Итак, P(|–|<e)=P_дов=(1–a), следовательно P(–e<<+e)=P_дов=(1–a).

Интервал (–e;+e), накрывающий неизвестный параметр  с заданной доверительной вероятностью P_дов=(1–a) называется доверительным интервалом.

Очевидно, что длина доверительного интервала определяется доверительной вероятностью P_дов=(1–a) и объемом выборки n. Проследить эти зависимости.

Таким образом интервальная оценка характеризует оцениваемый параметр  случайной величины x двумя числами ₁ и ₂ – концами доверительного интервала (₁ , ₂), который накрывает значение оцениваемого параметра  с заданной доверительной вероятностью.

Общая схема построения интервальных оценок параметров распределения и числовых характеристик случайных величин

Рассмотрим общий алгоритм построения доверительного интервала – интервальной оценки:

1.  По выборке объема n находится точечная оценка  числовой характеристики .

2.  Составляется вспомогательная СВ (выборочная статистика) Y, связанная с , и, имеющая известную ф.п.р.

3.  Для заданной доверительной вероятности P_дов=1–a находят интервал (Y₁ , Y₂ ), для которого P( Y₁ < Y < Y₂ )=P_дов=1–a.