Статистическая оценка неизвестных параметров распределения, страница 4

4.  Проводят обратное преобразование Y® и находят интервал (₁ , ₂ ), для которого P( ₁ <  < ₂ )=P_дов=1–a, который и является доверительным интервалом для оцениваемого параметра .

Сейчас мы рассмотрим примеры построения доверительных интервалов для некоторых числовых характеристик СВ, имеющей некоторые распределения. В некоторых случаях обоснуем применение той или иной вспомогательной СВ Y.

Построение доверительного интервала для математического ожидания СВ, имеющей нормальное распределение с известным среднеквадратическим отклонением

Пусть известно, что исследуемая СВ x имеет нормальное распределение

x~N(M[x],s[x]), 

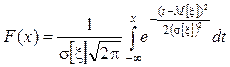
с известным СКО (s[x]). Значение МО (параметра M[x]) подлежит оценке.

Точечную оценку неизвестного МО можно найти по выборке объема n

.

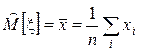Однако уже говорилось, что оценка  сами является СВ, поскольку для разных выборок она принимает различные значения.

Поскольку 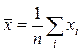 образуется как сумма значений x_i одной и той же СВ x, то в силу центральной предельной теоремы, СВ  имеет нормальный закон распределения. При этом МО СВ  равно M[x] (M[]=M[x]) на основании того, что оценка МО как  является несмещенной (см. выше). СКО СВ  (s[]) равно на основании свойств дисперсии СВ: D[Sh_i]=SD[h_i] и D[ch]=c²×D[h] (см. лекции за прошлый семестр):

.

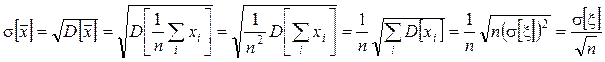Для построения доверительного интервала для параметра M[x] используется вспомогательная СВ, полученная из СВ  с помощью преобразования:

.

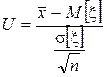Как и СВ  СВ U имеет нормальный закон распределения с математическим ожиданием:

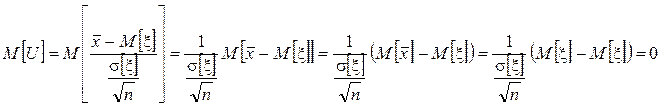
и дисперсией:

.

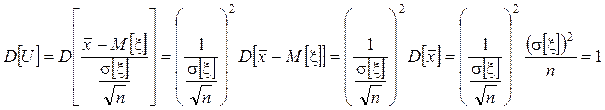Таким образом, СВ U~N(0,1), т.е. имеет стандартное нормальное распределение.

Значит, если  x~N(M[x],s[x]), то ~N(M[x], ), а U~N(0;1).

Для заданной доверительной вероятности P_дов=1–a найдем интервал (,) из условий:

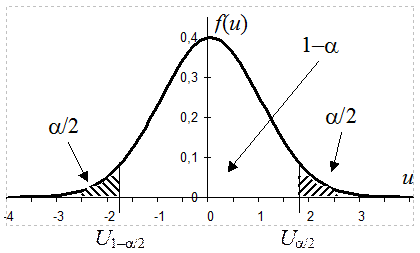
Значение СВ Y в котором значение ф.р. этой СВ равно 1–t  называется квантилем СВ Y уровня t и обозначается , т.е. F_Y()=1–t.

Квантили стандартной нормальной СВ U уровня (1-a/2) и (a/2) можно найти в специальных таблицах или из таблицы значений функции Лапласа на основе соотношения:

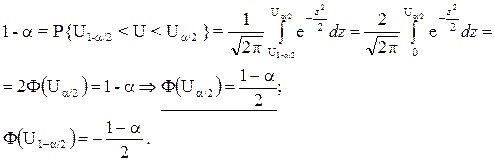
Найдя интервал (,) который с доверительной вероятностью накрывает значение U, можно найти доверительный интервал для МО M[x] следующим преобразованием:

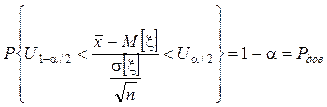 Þ 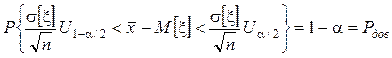 Þ

 Þ .

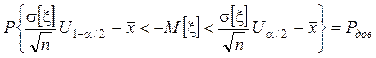Учитывая, что U_a/2=–U_1-a/2

.

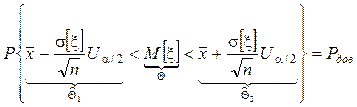Следовательно доверительный интервал для МО СВ, имеющей нормальное распределение с известным СКО найден. Абсолютная погрешность оценки равна: .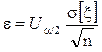

Построение доверительного интервала для МО СВ, имеющей нормальное распределение с неизвестным СКО

Пусть известно, что исследуемая СВ x имеет нормальное распределение x~ N(M[x],s[x]), а параметры распределения M[x] и s[x] неизвестны. Для нахождения оценок этих параметров извлечена выборка объема n и найдены их точечные оценки:

, .

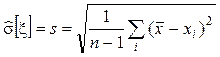Для построения доверительного интервала для МО СВ, имеющей нормальное распределение с неизвестным СКО, используется вспомогательная СВ (выборочная статистика) , которая имеет распределение Стьюдента с n=n–1 степенями свободы.

Таким образом, если  x~ N(M[x],s[x]), то t~t(n–1).

Для заданной доверительной вероятности P_дов=1–a найдем интервал (t_{1–a/2, n–1}, t_{a/2, n–1}) из условий:

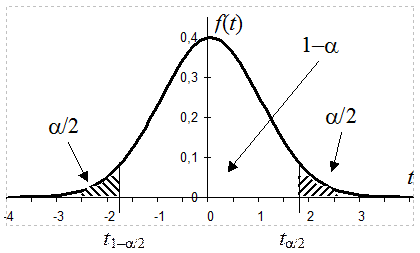
Квантили распределения Стьюдента уровня (1–a/2) и (a/2) для различного числа степеней свободы (n–1) можно найти в специальных таблицах. При этом следует учитывать, что на основании симметрии ф.п.р. распределения Стьюдента квантиль t_{1–a/2, n–1} = – t_{a/2, n–1} .