Статистическая оценка неизвестных параметров распределения, страница 5

Определив интервал (t_{1–a/2, n–1}, t_{a/2, n–1}), который с доверительной вероятностью накрывает значение t, можно найти доверительный интервал для МО M[x] следующим преобразованием:

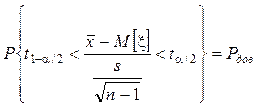 Þ  Þ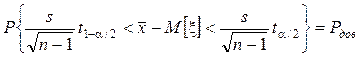

Þ Þ .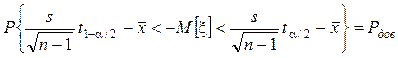

Учитывая, что t_a/2=–t_1-a/2

 .

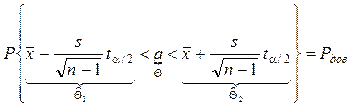Следовательно доверительный интервал для МО СВ, имеющей нормальное распределение с неизвестным СКО найден. Абсолютная погрешность оценки МО равна .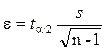

Построение доверительного интервала для СКО СВ, имеющей нормальное распределение

Пусть известно, что исследуемая СВ x имеет нормальное распределение x~N(M[x],s[x]), а параметры распределения M[x] и s[x] неизвестны. Предположим, что по выборке объема n найдены их точечные оценки:

, .

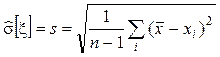Для построения доверительного интервала для СКО СВ, имеющей нормальное распределение, используется вспомогательная СВ (выборочная статистика) 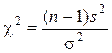, которая имеет распределение c²  с n=n-1 степенями свободы.

Таким образом, если  x~N(M[x],s[x]), то c² ~c² (n–1).

Для заданной доверительной вероятности P_дов=1–a, найдём интервал (c² _{1–a/2, n–1}, c² _{a/2, n–1}) из условий:

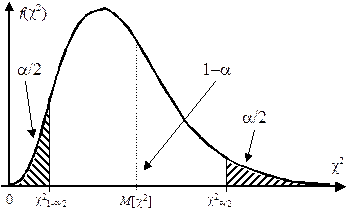
Квантили распределения c²  уровня (1-a/2) и (a/2) для различного числа степеней свободы (n–1) можно найти в специальных таблицах.

Определив интервал (c²_{1–a/2, n–1}, c²_a/2, n–1), который с доверительной вероятностью накрывает значение c² , можно найти доверительный интервал для СКО s[x] следующим преобразованием:

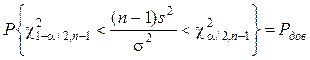 Þ  Þ

Þ  .

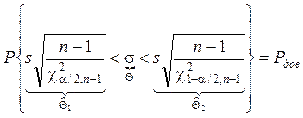Следовательно доверительный интервал для СКО СВ, имеющей нормальное распределение, найден.

Послесловие

На сегодняшней лекции мы рассмотрели методы статистической оценки параметров распределения и числовых характеристик СВ.

На следующей лекции мы перейдем к следующему важному разделу математической статистики, связанному с проверкой статистических гипотез, которому посвятим три лекции.

Оценки числовых характеристик случайных величин

Задача оценивания неизвестного параметра  распределения случайной величины x состоит в подборе приближенной функции V от элементов выборки {x₁, x₂,…x_n}: »V(x₁, x₂,…x_n), которую называют выборочной функцией (статистикой), а её значение: =V(x₁, x₂,…x_n) – оценкой параметра .

Точечная оценка  параметра распределения  (числовой характеристики) случайной величины x определяется одним числом =V(x₁, x₂,…x_n).

Точечная оценка параметра =V(x₁, x₂,…x_n) называется состоятельной, если 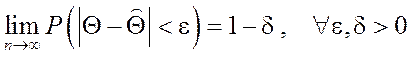, где e и d – произвольные сколь угодно малые положительные числа.

Точечная оценка параметра  является несмещенной, если  .

Точечная оценка параметра  называется асимптотически несмещенной, если  .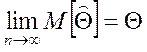

Точечная несмещенная оценка параметра =V(x₁, x₂,…x_n) называется эффективной, если она обладает минимальной дисперсией среди других возможных оценок исследуемого параметра.

Пусть {x₁, x₂,…x_n} – выборка значений СВ x. Значения элементов выборки можно рассматривать как n случайных величин, каждая их которых имеет распределение F_x(x) с математическим ожиданием M[x].

Вычислим математическое ожидание оценки :

.

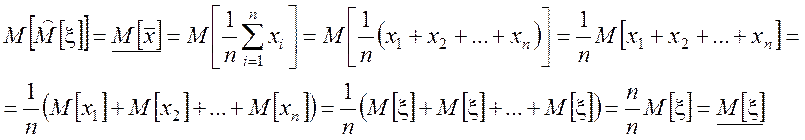Доказательство свойства состоятельности оценки МО как среднего арифметического следует непосредственно из теоремы Чебышева: при достаточно большом числе независимых опытов среднее арифметическое наблюдаемых значений случайной величины x сходится по вероятности к её математическому ожиданию, т.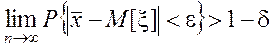е. , где  – среднее арифметическое наблюдаемых значений СВ x, а  e и d – произвольные сколь угодно малые положительные числа.

Интервальная оценка характеризует оцениваемый параметр  случайной величины x двумя числами ₁ и ₂ – концами интервала (₁ , ₂), который накрывает значение оцениваемого параметра  с заданной вероятностью.