










Федеральное государственное бюджетное образовательное
Учреждение высшего профессионального образования
«Дальневосточный государственный университет путей сообщения»
Кафедра «БУ и аудит»
Контрольная работа по дисциплине: «Эконометрика»
Вариант:№7
Выполнил студент 4 курса ИИФО:
Одиноков Иван Михайлович
Шифр: КА11-Э-757
Проверил: Кобозев Анатолий Васильевич
Хабаровск
2011
Задача 7
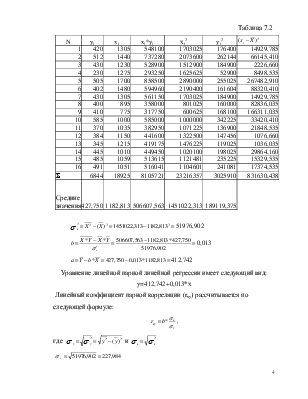
Имеются данные о потребительских расходах на душу населения (y, руб.), средней заработной плате и социальных выплатах (x, руб.) по 16 районам региона. Данные приведены в табл. 7.1.
Таблица 7.1
|
Районы |
y |
x |
|
1 |
420 |
1305 |
|
2 |
512 |
1440 |
|
3 |
430 |
1230 |
|
4 |
230 |
1275 |
|
5 |
505 |
1700 |
|
6 |
402 |
1480 |
|
7 |
430 |
1305 |
|
8 |
400 |
895 |
|
9 |
410 |
775 |
|
10 |
585 |
1000 |
|
11 |
370 |
1035 |
|
12 |
384 |
1150 |
|
13 |
345 |
1215 |
|
14 |
445 |
1010 |
|
15 |
485 |
1059 |
|
16 |
491 |
1051 |
1) Рассчитать параметры уравнений
регрессии y=a+b*x+e и y=a+b*![]() +e.
+e.
2) Оценить тесноту связи с помощью индексов корреляции и детерминации.
3) Рассчитать средний коэффициент эластичности и дать сравнительную оценку силы связи фактора с результатом.
4) Рассчитайте среднюю ошибку аппроксимации и оцените качество модели.
5) С помощью F-статистики Фишера (при a=0,01) оценить надежность уравнения регрессией
6) Рассчитайте прогнозное значение yпр, если прогнозное значение фактора увеличится на 5% от его среднего значения. Определите доверительный интервал прогноза для a=0,01.
7) Расчеты должны быть подробны и сопровождены пояснительной запиской.
Решение.
Оценки параметров линейной регрессии y=a+b*x могут быть рассчитаны по следующим формулам:
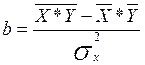 и
и ![]() ,
,
где 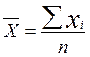 - среднее значение факторного признака
- среднее значение факторного признака
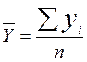 - среднее значение результативного признака
- среднее значение результативного признака
n - количество наблюдений в выборочной совокупности
![]() - дисперсия факторного признака
- дисперсия факторного признака
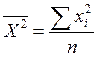
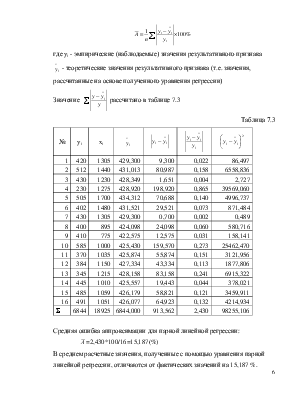
Значения Sх, Sy, Sх2, Sy*х, ![]() и s2
рассчитаны в таблице 7.2
и s2
рассчитаны в таблице 7.2
Таблица 7.2
|
N |
yi |
xi |
xi*yi |
хi2 |
yi2 |
|
|
1 |
420 |
1305 |
548100 |
1703025 |
176400 |
14929,785 |
|
2 |
512 |
1440 |
737280 |
2073600 |
262144 |
66145,410 |
|
3 |
430 |
1230 |
528900 |
1512900 |
184900 |
2226,660 |
|
4 |
230 |
1275 |
293250 |
1625625 |
52900 |
8498,535 |
|
5 |
505 |
1700 |
858500 |
2890000 |
255025 |
267482,910 |
|
6 |
402 |
1480 |
594960 |
2190400 |
161604 |
88320,410 |
|
7 |
430 |
1305 |
561150 |
1703025 |
184900 |
14929,785 |
|
8 |
400 |
895 |
358000 |
801025 |
160000 |
82836,035 |
|
9 |
410 |
775 |
317750 |
600625 |
168100 |
166311,035 |
|
10 |
585 |
1000 |
585000 |
1000000 |
342225 |
33420,410 |
|
11 |
370 |
1035 |
382950 |
1071225 |
136900 |
21848,535 |
|
12 |
384 |
1150 |
441600 |
1322500 |
147456 |
1076,660 |
|
13 |
345 |
1215 |
419175 |
1476225 |
119025 |
1036,035 |
|
14 |
445 |
1010 |
449450 |
1020100 |
198025 |
29864,160 |
|
15 |
485 |
1059 |
513615 |
1121481 |
235225 |
15329,535 |
|
16 |
491 |
1051 |
516041 |
1104601 |
241081 |
17374,535 |
|
S |
6844 |
18925 |
8105721 |
23216357 |
3025910 |
831630,438 |
|
Средние значения |
427,750 |
1182,813 |
506607,563 |
1451022,313 |
189119,375 |
![]() 51976,902
51976,902
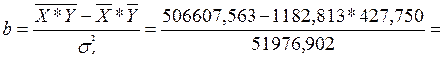 0,013
0,013
![]() 412,742
412,742
Уравнение линейной парной линейной регрессии имеет следующий вид: y=412,742+0,013*х
Линейный коэффициент парной корреляции (rxy) рассчитывается по следующей формуле:
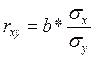 ,
,
где ![]() и
и ![]()
![]()
![]()
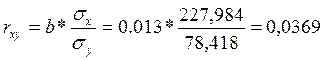
Значение коэффициента корреляции близко к нулю, поэтому можно утверждать, что связь между признаками отсутствует.
Коэффициент детерминации (r2xy):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.