Расчет параметров уравнения регрессии y=a+bx+ε по данным рынка вторичного жилья

ГОУ ВПО

Дальневосточный государственный университет путей сообщения

Кафедра “Бухгалтерский учет и аудит”

Контрольная работа

По дисциплине: Эконометрика

                                                           Выполнила: Кабанова Е.М.

                                                                                                КПО7-Э-031                                                                                 

                                                                   Проверила: Корзова Л.Н.

Хабаровск

2009
Контрольное задание №1.

Имеются данные за 12 месяцев года по району города о рынке вторичного жилья: стоимость квартиры (y , тыс. у.е.;), размер общей площади (x, ).

1. Расчет параметров уравнений регрессий

Найдем средние значения соответствующих величин:

, , 

, ,  ,

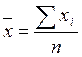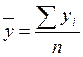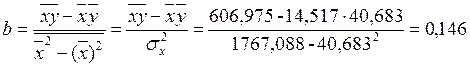
Линейное уравнение регрессии имеет вид:

2. Оценка тесноты связи с помощью индексов корреляции и детерминации.

Рассчитаем линейный коэффициент парной корреляции:

,

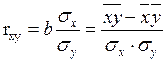где  ,

       ;

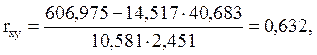
Коэффициент корреляции показывает тесноту связей между фактором и результативным признаком и обладает свойством

Т.к. , то

Т.к. по расчету коэффициент корреляции близок к единице – это означает линейная связь между признаками заметна.

Коэффициент детерминации характеризует долю дисперсии признака у, объясненную регрессией, в общий дисперсии признака у и определяется:

Следовательно, 40 % результата объясняется вариацией объясняющей переменной х.

3. Расчет среднего коэффициента эластичности и сравнительная оценка силы связи фактора с результатом.

       Коэффициент эластичности показывает, на сколько процентов изменится величина результативного признака y при изменении признака-фактора x на 1%.

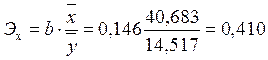
Это означает что при увеличении общей площади квартиры на 1% стоимость квартиры возрастет на  0,410 %

4. Расчет средней ошибки аппроксимации и оценка качества модели.

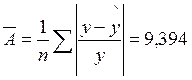
Средняя ошибка аппроксимации не вышла за допустимые пределы (8-10%), что говорит о удачном выборе модели регрессии.

5. Оценка надежности регрессии уравнения с помощью F-статистики Фишера (при a=0,05).

Рассчитаем значение F-критерия Фишера:

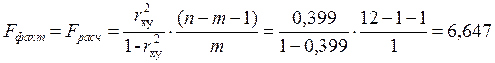
Находим

Так как F_факт>F_табл, то гипотеза H₀ о статической незначимости параметра b в уравнении регрессии отклоняется. Уравнение регрессии является статически значимым.

6. Расчет прогнозного значения  , если прогнозное значение фактора увеличится на 5% от его среднего значения. Определение доверительного интервала прогноза для a=0,05.

Рассчитаем

Рассчитаем стандартную ошибку:

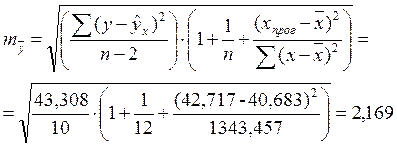
Доверительный интервал прогноза:    ()

t_табл= t(a=0,05; v=10) = 2,228

14,814-2,228×2,169<<14,814+2,228×2,169

9,981<<19,647

1. Расчет параметров уравнений регрессий

Произведя замену z=, получим уравнение

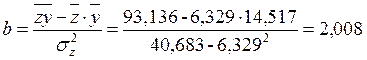
Линейное уравнение регрессии имеет вид:

2. Оценка тесноты связи с помощью индексов корреляции и детерминации.

Рассчитаем линейный коэффициент парной корреляции:

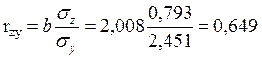
так как значение коэффициента близко к единице, то связь между признаками y и k заметна.

Коэффициент детерминации:

3. Расчет среднего коэффициента эластичности и сравнительная оценка силы связи фактора с результатом.

       Коэффициент эластичности показывает, на сколько процентов изменится величина результативного признака y при изменении признака-фактора k на 1%.

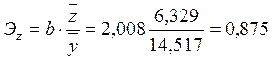
Это означает что при увеличении общей площади квартиры на 1% стоимость квартиры возрастает на  0,875 %

4. Расчет средней ошибки аппроксимации и оценка качества модели.

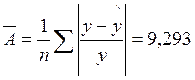
Средняя ошибка аппроксимации не вышла за допустимые пределы (8-10%), что говорит о удачном выборе модели регрессии.

5. Оценка надежности регрессии уравнения с помощью F-статистики Фишера (при a=0,05).

Рассчитаем значение F-критерия Фишера:

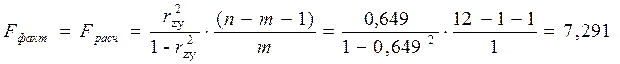
Находим

Так как F_факт>F_табл, то гипотеза H₀ о статической незначимости параметра b в уравнении регрессии не принимается. Уравнение регрессии статически значимо.

6. Расчет прогнозного значения  , если прогнозное значение фактора