Расчет параметров уравнения регрессии y=a+b√x+ε. Оценка тесноты связи с помощью индексов корреляции и детерминации

Рассчитать средний коэффициент эластичности и дать сравнительную оценку силы связи фактора с результатом.

4.  Рассчитать среднюю ошибку аппроксимации и оценить качество модели.

5.  С помощью F-статистики Фишера (при α=0,05) оценить надёжность регрессии уравнения.

6.  Рассчитать прогнозное значение , если прогнозное значение фактора увеличится на 5 % от его среднего значения. Определить доверительный интервал прогноза для α=0,05.

Решение: Составим расчётную таблицу (таблица 1), расчёты ведём по формулам:

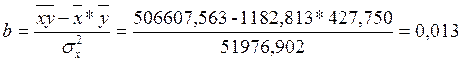
Линейное уравнение регрессии имеет вид .

Рассчитаем линейный коэффициент парной корреляции:

,

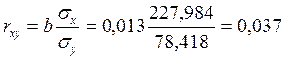Так как значение коэффициента корреляции близко к нулю, связь между признаками х и у слабая.

Рассчитаем значение F-критерия Фишера

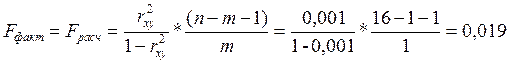
По таблице приложения 1 в методическом указании находим

Так как F_расч<F_табл, то гипотеза об отсутствии линейной связи между признаками (H₀:b=0) подтверждается.

Так как  = 0,001 (коэффициент детерминации), это означает, что 0,1% результата объясняется вариациями объясняющей переменной.

Для оценки качества модели рассчитаем среднюю ошибку аппроксимации:

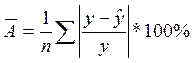= 15,197 %, то, что средняя ошибка аппроксимации вышла за допустимые пределы (8-10%), это говорит о неудачном выборе модели регрессии.

Выберем в качестве модели уравнение регрессии , предварительно линеаризировав модель, для этого обозначим , получим линейное уравнение парной регрессии .

Все промежуточные расчёты поместим в таблицу 2.

Расчёты ведём по формулам:

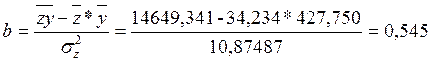
Уравнение регрессии имеет вид .

Коэффициент корреляции

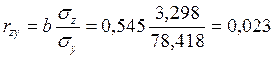
Так как значение коэффициента корреляции близко к нулю, связь между признаками z и у слабая.

Так как  = 0,001 (коэффициент детерминации), это означает, что 0,1% результата объясняется вариациями объясняющей переменной.

Рассчитаем значение F-критерия Фишера

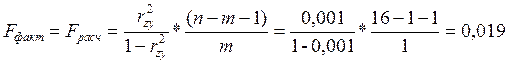
По таблице приложения 1 в методическом указании находим

Так как F_расч<F_табл, то гипотеза об отсутствии линейной связи между признаками (H₀:b=0) подтверждается.

Для оценки качества модели рассчитаем среднюю ошибку аппроксимации:

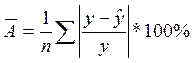= 15,227 %, то, что средняя ошибка аппроксимации вышла за допустимые пределы (8-10%), это говорит о неудачном выборе модели регрессии.

Вывод: Оба уравнения регрессии статистически незначимы в целом.

Задача 17

Имеются данные за 12 месяцев по району города о рынке вторичного жилья, (у – стоимость квартиры, тыс. у.е.; х₁ – размер жилой площади, м²; х₂ – размер кухни, м²).

у	х1	х2
13,2	46,0	5,8
15,9	54,1	8,5
16,2	50,6	8,0
15,4	43,8	5,2
14,2	78,6	12,0
11,0	60,2	7,2
21,1	50,2	7,0
13,4	54,7	7,3
15,6	42,8	5,5
12,8	60,4	7,3
14,5	47,2	5,8
15,1	40,6	5,2

Задание:

1.  Рассчитать параметры линейного уравнений множественной регрессии.

2.  Дайте оценку силы связи факторов с результатом с помощью среднего коэффициента эластичности.

3.  Оцените статистическую значимость параметров и уравнения регрессии в целом с помощью соответственно критериев Стьюдента и Фишера (α=0,01).

4.  Рассчитать среднюю ошибку аппроксимации. Сделайте вывод.

5.  Составьте матрицы парных и частных коэффициентов корреляции и укажите информативные факторы.

6.  Оцените полученные результаты, выводы оформите в аналитической записке.

Решение: Составим расчётную таблицу (таблица 3), рассмотрим уравнение вида Y=а+b₁x₁+b₂x₂+ε

Параметры уравнения можно найти из решения системы уравнений:

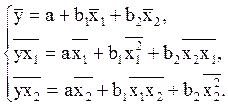
Или, перейдя к уравнению в стандартизированном масштабе:

, где 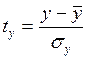,  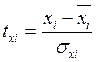- стандартизированные переменные;  - стандартизированные коэффициенты,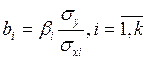

Коэффициенты , в частности для k=2, определяются из системы уравнений:

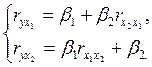
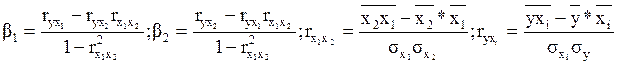
Подставив данные, получим:

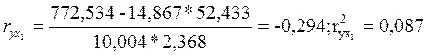
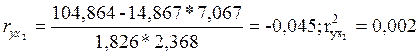
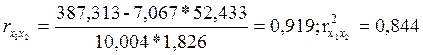
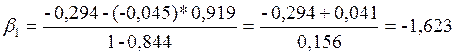
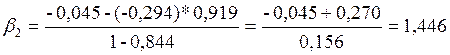
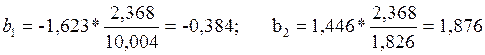
Стандартизированная форма уравнения регрессии имеет вид:

Естественная форма уравнения регрессии имеет вид

Для выяснения относительной силы влияния факторов на результативный признак рассчитаем средние коэффициенты эластичности:

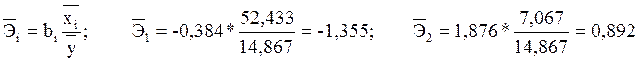
Следовательно, при увеличении размера жилой площади