Расчет параметров уравнений регрессий y=a+b*x+e и y=a+b√x+е (по данным о потребительских расходах на душу населения), страница 3

g_Yп=Y_п±D_Yп

g_Yп=Y_п-D_Yп

g_Yп=Y_п+D_Yп

Значение 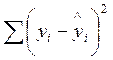 рассчитано в таблице 7.3

Значение  рассчитано в таблице 7.2

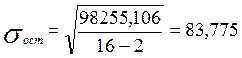
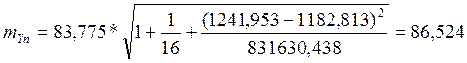
При n=16 и m=2 число степеней свободы n=n-m=16-2=14

При уровне значимости a=0.01  и n=14 коэффициент доверия   t_a =2,9768

Предельная ошибка прогноза, которая не будет превышена в 99 %

случаев составит:

Dg_Yп =2,9768*86,524=257,564

  Строим доверительный интервал, т.е. интервал, включающий в себя оцениваемое значение с вероятностью 1-a=1-0,01=0,99.

Доверительный интервал прогноза, полученного на основе парной линейной регрессии y=412.742+0.013*x:

               g_Yп=428.500±257.564

               g_Yп(min)=428.500-257.564=170,936

               g_Yп(max)=428.500+257.564=686,065

              D_g=g_Yп(max)/g_Yп(min)=686.065/170.936=4,014

Рассчитанный прогноз уровня потребительских расходов является надежным, но не достаточно точным, потому что верхняя граница доверительного интервала прогноза больше его нижней границы в 4.014 раза.

 Для построения уравнение регрессии y=a+b* произведем замену z=. Тогда: y=a+b*z

Для расчета оценок параметров а и b используем данные таблицы 7.4

Таблица 7.4

10,875

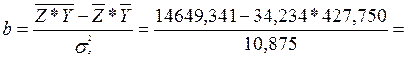0,545

409,085

Уравнение с переменной z: y=409,085+0,545*z

После обратной замены получим уравнение: y=409,085+0,545*

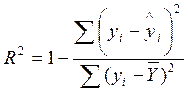Для нелинейной регрессии индекс детерминации (R²) рассчитывается по следующей формуле:

Значения 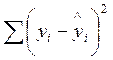, рассчитаны в таблице 7.5

Таблица 7.5