Расчет параметров уравнений регрессий y=a+b*x+e и y=a+b√x+е (по данным о потребительских расходах на душу населения), страница 2

         r²_xy=0,0369²=0,0014

Полученное значение коэффициента детерминации означает, что парная линейная регрессия вида Y=412.742+0.013*x объясняет только 0.14 % общей вариации результативного признака,

остальные 99.86% (100-0.14=99.86) вариации результативного  признака объясняются изменением факторов, не включенных в модель.

Средний коэффициент эластичности  показывает, на сколько процентов в среднем по совокупности изменится значение результативного признака от своей средней величины при изменении факторного признака на 1% от своего среднего значения. Значение среднего коэффициента эластичности определяется по  формуле:

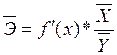
где f'(x) - первая производная уравнения регрессии по х

Для уравнения парной линейной регрессии Y=412.742+0.013*x

f'(x)=0,013

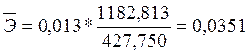
   В модели парной линейной регрессии при изменении среднего значения заработной платы и социальных выплат на 1% уровень потребительских расходов в среднем по совокупности изменится на 0.0351 % от своего среднего значения.

Средняя ошибка аппроксимации   определяется по формуле:

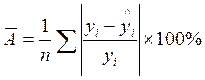
где y_i - эмпирические (наблюдаемые) значения результативного признака

 - теоретические значения результативного признака (т.е. значения, рассчитанные на основе полученного уравнения регрессии)

Значение 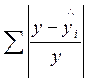  рассчитано в таблице 7.3

Таблица 7.3

Средняя ошибка аппроксимации для парной линейной регрессии:

                =2,430*100/16=15,187(%)

В среднем расчетные значения, полученные с помощью уравнения парной линейной регрессии, отличаются от фактических значений на 15,187 %. Значение средней ошибки аппроксимации вышло за пределы допустимых значений (8%-10%), что говорит о неудачном выборе модели регрессии.

    Рассчитаем значение F-критерия Фишера по формуле:

,

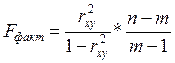где n-объем выборки

m-количество оцениваемых параметров в уравнении регрессии

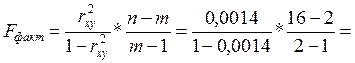0,0191

Расчетное значение F сопоставляется с табличным (критическим) значением, определяемым для числа степеней свободы n₁=m-1 и n₂=n-m и заданного уровня значимости a.

Критическое значение F-критерия при a=0,01; n₁=2-1=1; n₂=16-2=14 равно 8,86

Так как F_факт<F_крит, то принимается гипотеза H0 о статистической незначимости уравнения парной линейной регрессии (это означает, что оценки параметров а и b сформировались под воздействием  случайных факторов).

Х_п=*1.05=1182,813*1.05=1241,953 (руб.) - значение факторного признака при его увеличении на 5% от исходного среднего уровня.

Прогнозное значение результативного признака (Y_п) определяется путем подстановки в соответствующее уравнение регрессии прогнозного значения факторного признака (Х_п).

Уравнение линейной регрессии Y=412,742+0,013*x

  Тогда Y_п=412,742+0,013*1241,953=428,500 (руб.)

Затем вычисляется средняя стандартная ошибка прогноза (m_Yп):

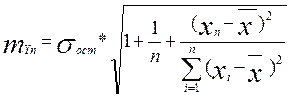
где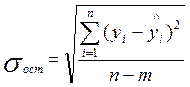

Предельная ошибка прогноза (D_Yп):

D_Yп=t_табл(a,n)*m_Yп

   Доверительный интервал прогноза (g_Yп):