Расчет параметров уравнений регрессий y=a+b*x+e и y=a+b√x+е (по данным о потребительских расходах на душу населения), страница 4

R²=1-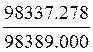=0,0005

Полученное значение коэффициента детерминации означает, что парная  регрессия вида y=409,085+0,545* объясняет только 0.05 % общей вариации результативного признака, остальные  99.95% (100-0.05=99.95) вариации результативного признака объясняются изменением факторов, не включенных в модель.

Определим индекс корреляции (R) :

Значение коэффициента корреляции близко к нулю, поэтому можно утверждать, что связь между признаками отсутствует.

Далее рассчитаем значение среднего коэффициента эластичности.

Для уравнения  регрессии  y=409,085+0,545*

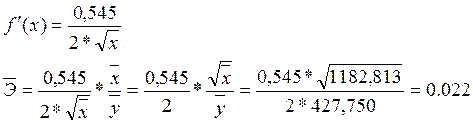
В модели парной регрессии y=409,085+0,545* при изменении среднего значения заработной платы и социальных выплат на 1% уровень  потребительских расходов в среднем по совокупности изменится на 0.022 % от своего среднего значения.

Значение 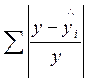,  необходимое для определения средней ошибки аппроксимации рассчитаны в таблице 7.5.

Средняя ошибка аппроксимации для парной регрессии y=409,085+0,545*:

                =2,436*100/16=15,228 (%)

То есть, в среднем расчетные значения, полученные с помощью уравнения парной  регрессии  y=409,085+0,545* , отличаются от фактических  значений на 15,228 %.  Значение средней ошибки аппроксимации вышло за пределы допустимых значений (8%-10%), что говорит о неудачном выборе модели регрессии.

    Рассчитаем значение F-критерия Фишера

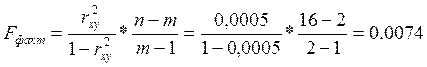
n-объем выборки

m-количество оцениваемых параметров в уравнении регрессии

Расчетное значение F сопоставляется с табличным (критическим) значением, определяемым для числа степеней свободы n₁=m-1 и n₂=n-m и заданного уровня значимости a.

Критическое значение F-критерия при a=0,01; n₁=2-1=1; n₂=16-2=14 равно 8,86

Так как F_факт<F_крит, то принимается гипотеза H₀ о статистической незначимости уравнения регрессии y=409,085+0,545* (это означает, что оценки параметров а и b сформировались под воздействием  случайных факторов).

   Х_п=*1.05=1182,813*1.05=1241,953 (руб.) - значение факторного признака при его увеличении на 5% от исходного среднего уровня.

Прогнозное значение результативного признака (Y_п) определяется

путем подстановки в соответствующее уравнение регрессии

прогнозного значения факторного признака (Х_п):

     Тогда Y_п= y=409,085+0,545*=428,299 (руб.)

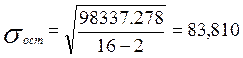
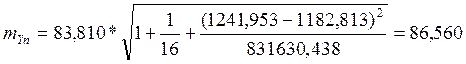
При n=16 и m=2 число степеней свободы n=n-m=16-2=14

При уровне значимости a=0.01  и n=14 коэффициент доверия   t_a =2,9768

Предельная ошибка прогноза, которая не будет превышена в 99 %

случаев составит:

Dg_Yп =2,9768*86,560=257,672

Строим доверительный интервал, т.е. интервал, включающий в себя оцениваемое значение с вероятностью 1-a=1-0,01=0,99.

Доверительный интервал прогноза, полученного на основе парной  регрессии y=409,085+0,545*:

              g_Yп=428.299±257.672

              g_Yп(min)=428.299-257.672=170,628

               g_Yп(max)=428.299+257.672=685,971

              D_g=g_Yп(max)/g_Yп(min)=685.971/170.628=4,020

Рассчитанный прогноз уровня потребительских расходов является надежным, но не достаточно точным, потому что верхняя граница доверительного интервала прогноза больше его нижней границы в 4.020 раза.

  На основе проведенных расчетов можно сделать следующие выводы.

  Оба уравнения регрессии характеризуются очень низким значением коэффициента детерминации и коэффициента корреляции. Это свидетельствует о том, что модель построена на основе фактора, не имеющей существенной связи с результативным признаком.

  Об этом так же свидетельствуют небольшие значения коэффициентов средней эластичности (для обоих видов регрессии средний коэффициент эластичности не превышает значения 0.04 %).

  Оба уравнения регрессии характеризуются значительной величиной средней ошибки аппроксимации, что свидетельствует о недостаточной точности рассчитываемых теоретических значений результативного признака.

  Критическое значение F-критерия Фишера больше величин его фактических значений для обоих моделей, следовательно, ни одна из них не является статистически значимой, т.е. следует принять гипотезу об отсутствии реальной связи между уровнем потребительских расходов и уровнем заработной платы и социальных выплат.Поэтому ни одна из полученных моделей регрессии не может использоваться для практических расчетов.