Расчет параметров линейного уравнения множественной регрессии (по данным о деятельности крупнейших кампаний), страница 7

=(30+52+47+28+16+51+40+35+57+28+33+42+39)/13=498/13=38,308

 =(29+40+30+52+47+28+16+51+40+35+57+28+33)/13=486/13=37,385

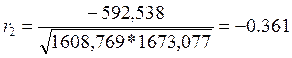
Коэффициент корреляции второго порядка так же свидетельствует о незначительной линейной зависимости между количеством посещений, имевших  место в течение дня t, и количеством посещений, произошедших в течение дня t-2.

Динамика посещений не позволяет осуществить аналитическое выравнивание ряда на основе линейной регрессии вида y=a₀+a₁*t. Поэтому определим параметры уравнения тренда, описываемого полулогарифмической  функцией: y=a₀+a₁*lg(t).

 Параметры полулогарифмической функции y=a₀+a₁*lg(t)определяются

при решении системы нормальных уравнений, отвечающих требованию

МНК.

n*a₀+a₁*Slg(t)=Sy

a₀*Slg(t)+a₁*S(lg(t))²=S(y*lg(t))

Расчет значений Slg(t), S(lg(t))², S(y*lg(t)) и Sy произведем в  таблице 31.4

Таблица 31.4

N	yi	lg(ti)	lg(ti)*yi	(lg(ti))2
1	29	0,000	0,000	0,000	34,104	26,048	77,440
2	40	0,301	12,041	0,091	35,481	20,419	4,840
3	30	0,477	14,314	0,228	36,287	39,526	60,840
4	52	0,602	31,307	0,362	36,859	229,259	201,640
5	47	0,699	32,852	0,489	37,302	94,048	84,640
6	28	0,778	21,788	0,606	37,664	93,402	96,040
7	16	0,845	13,522	0,714	37,971	482,717	475,240
8	51	0,903	46,058	0,816	38,236	162,915	174,240
9	40	0,954	38,170	0,911	38,470	2,340	4,840
10	35	1,000	35,000	1,000	38,680	13,540	7,840
11	57	1,041	59,359	1,084	38,869	328,731	368,640
12	28	1,079	30,217	1,165	39,042	121,925	96,040
13	33	1,114	36,760	1,241	39,201	38,453	23,040
14	42	1,146	48,137	1,314	39,348	7,031	17,640
15	39	1,176	45,868	1,383	39,485	0,236	1,440
S	567	12,116	465,392	11,402	567,000	1660,591	1694,400

Применительно к результатам расчетов, проведенных в таблице 31.4составим систему нормальных уравнений, при решении которой определяются параметры полулогарифмической функции a₀ и а₁:

15*a₀+12.116*a₁=567

12.116*a₀+11.402*a₁=465,392

 Параметры уравнения полулогарифмической функции, полученные

при решении указанной системы уравнений:

a₁=4,5759

a₀=34,1038

Тогда уравнение тренда, выраженное в виде полулогарифмической функции, записывается следующим образом:

       y=34,1038+4,5759*lg(t)

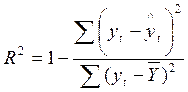Для полученного уравнения тренда рассчитаем значение коэффициента детерминации (R²):

 

     - теоретические уровни ряда, рассчитанные на основе полученного уравнения тренда       y=34,1038+4,5759*lg(t)

 

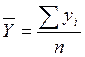                 =567/15=37,800

 

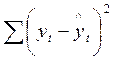Значения                       и                     рассчитаны в таблице 31.4

       R²=1-1660,591/1694,400=0,020

Рассчитанное значение коэффициента детерминации означает, что полученное уравнение тренда объясняет только 2,00 % изменений в анализируемом временном ряду, поэтому данное уравнение тренда не может быть использовано для получения адекватных прогнозов.

Список источников

1. Доугерти К. Введение в эконометрику. - М.: Финансы и статистика, 1999.

 2. Магнус Я. Р., Катышев П. К., Пересетский А. А. Эконометрика. Начальный курс. - М.: Дело, 2000.

 3. Эконометрика. Учебник. (Под ред. И. И. Елисеевой). - М.: Финансы и статистика, 2001