Расчет параметров линейного уравнения множественной регрессии (по данным о деятельности крупнейших кампаний), страница 2

 

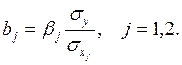
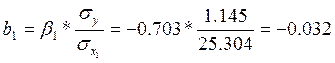
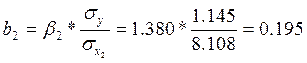
Уравнение множественной регрессии в естественной форме выглядит следующим образом: Y=0,693-0.032*x₁+0,195*x₂

2) Для выяснения относительной силы влияния факторов на результативный фактор рассчитываются средние коэффициенты эластичности :

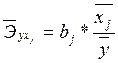
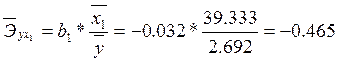
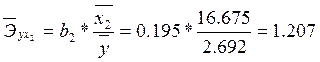
Частные коэффициенты эластичности показывают, что при изменении оборота капитала (фактора х₁) на 1 % от среднего значения чистый доход компании изменится на 0,465 % от своего среднего значения, а при  изменении объема использованного капитала (фактор х₂) на 1 % от среднего значения чистый доход компании изменится на 1,207 % от своего среднего значения.

=0.465<=1,207, следовательно, фактор х₂ (объем использованного капитала) оказывает на результативный признак большее влияние, чем фактор х₁ (оборот капитала). Этот вывод подтверждается соотношением стандартизованных коэффициентов b₁ и b₂:

 |b₁|=0,703<|b₂|=1,380

3) Для проверки статистической значимости параметров регрессии и уравнения регрессии в целом следует рассчитать коэффициент множественной детерминации.

Линейный коэффициент множественной детерминации (R²_yx1x2) рассчитывается по формуле:

 

 R²_yx1x2=0.535*(-0.703)+0.750*1.380=0,659

Рассчитанное значение коэффициента множественной детерминации означает, что 65,9 % изменений результативного признака (уровень чистого дохода) объясняется изменениями факторных признаков (оборот капитала и объем использованного капитала). Остальные 34,1 % вариации результативного признака объясняются воздействием факторов, не включенных в  синтезированную модель.

Линейный коэффициент множественной корреляции R_yx1x2 рассчитывается по формуле:

Величина коэффициента множественной корреляции характеризует силу связи между признаками в синтезированной модели в соответствии со шкалой Чеддока как высокую.

    Рассчитаем значение F-критерия Фишера

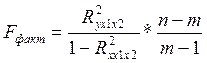
n-объем выборки

m-количество оцениваемых параметров в уравнении регрессии

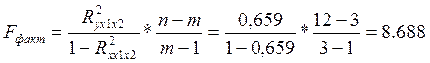
Расчетное значение F сопоставляется с табличным (критическим) значением, определяемым для числа степеней свободы n₁=m-1 и n₂=n-m и заданного уровня значимости a.

Критическое значение F-критерия при a=0,01; n₁=3-1=2; n₂=12-3=9

равно 8.02

F_факт=8,688>F_крит=8.02,  поэтому уравнение двухфакторной линейной регрессии является статистически значимым на 1%-ном уровне значимости.

Значимость коэффициентов регрессии можно проверить с помощью критерия Стьюдента. Для этого для коэффициента регрессии b_j рассчитывается фактическое значение t-статистики (t_bj):

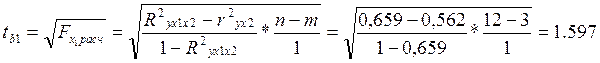
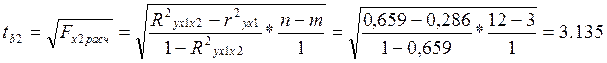
Полученные расчетные значения критерия Стьюдента сравниваются с табличным значением (t_табл) для уровня значимости a и числа степеней свободы n=n-m.

t_табл(a=0.01; n=12-3=9)=3.2498

Для коэффициента регрессии b₁ расчетное значение критерия Стьюдента меньше табличного, что свидетельствует о незначимости коэффициента регрессии b₁ и неинформативности факторного признака x₁.

Для коэффициента регрессии b₂ расчетное значение критерия Стьюдента  так же меньше табличного, что является основанием для вывода о о статистической незначимости коэффициента регрессии b₂ при  1%-ном уровне значимости.

4) Средняя ошибка аппроксимации   рассчитывается по формуле:

 

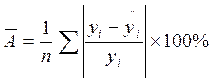где y_i - эмпирические (наблюдаемые) значения результативного признака;

    - теоретические (рассчитанные при помощи найденного уравнения регрессии) значения результативного признака

Значение 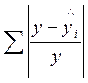  , необходимое для определения средней ошибки аппроксимации рассчитаны в таблице 11.3)

Таблица 11.3

N	y	x1	x2
1	5,500	53,100	27,100	4,285	1,215	0,221
2	2,400	18,800	11,200	2,278	0,122	0,051
3	3,000	35,300	16,400	2,766	0,234	0,078
4	4,200	71,900	32,500	4,740	0,540	0,129
5	2,700	93,600	25,400	2,666	0,034	0,013
6	1,600	10,000	6,400	1,622	0,022	0,014
7	2,400	31,500	12,500	2,127	0,273	0,114
8	3,300	36,700	14,300	2,313	0,987	0,299
9	1,800	13,800	6,500	1,521	0,279	0,155
10	2,400	64,800	22,700	3,056	0,656	0,273
11	1,600	30,400	15,800	2,805	1,205	0,753
12	1,400	12,100	9,300	2,121	0,721	0,515
S	32,300	472,000	200,100	32,300	6,288	2,614