Расчет параметров линейного уравнения множественной регрессии (по данным о деятельности крупнейших кампаний), страница 5

   Проверим выполнение достаточного условия идентификации для третьего уравнения.

   В третьем уравнении отсутствуют следующие переменные: C_t, J_t, G_t, Y_t-1.

Составим матрицу из коэффициентов при этих переменных, находящихся в других уравнения системы (1-ом, 2-ом и 4-ом):

Ранг матрицы равен трем, т.е. равен числу эндогенных переменных системы без 1, так как определитель квадратной подматрицы 3х3 этой матрицы не равен нулю:

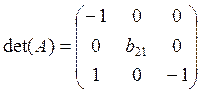=(-1)*b₂₁*(-1)+0*0*0+0*0*1-1*b₂₁*0-(-1)*0*0-

-0*0*(-1)=b₂₁¹0

Таким образом, достаточное условие идентификации для третьего уравнения выполняется, следовательно, третье уравнение системы является сверхидентифицированным.

  Четвертое уравнение представляет собой тождество, параметры  которого известны, поэтому необходимость в его идентификации отсутствует.

      Таким образом, в анализируемой системе 1-ое уравнение точно идентифицируемо, а 2-ое и 3-е уравнения являются сверхидентифицируемыми.

  Система, в которой хотя бы одно уравнение сверхидентифицировано,  а другие уравнения точно идентифицированы является сверхидентифицированной.

  Для оценки параметров сверхидентифицированной системы используется двухшаговый метод наименьших квадратов (ДМНК).

  Двухшаговый метод наименьших квадратов заключается в следующем:

   1) составляют приведенную форму модели и определяют численные значения параметров каждого ее уравнения обычным методом наименьших квадратов;

   2) выявляют эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяются двухшаговым методом наименьших квадратов, и находят расчетные значения по соответствующим уравнениям приведенной формы модели;

   3) обычным методом наименьших квадратов определяют параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения  эндогенных переменных, стоящих в правой части данного структурного уравнения.

Задача 31

Имеются данные за 15 дней по количеству пациентов клиники, прошедших

через терапевтическое отделение в течение  дня (таблица 31.1)

Таблица 31.1

1) Определить коэффициенты автокорреляции уровней первого и второго порядков;

2) обосновать выбор уравнения тренда и определить его параметры;

3) сделать выводы;

4) результаты оформить в виде пояснительной записки.

Решение.

1.) Определим коэффициент корреляции между рядами y_t  и y_t-1 (r₁).

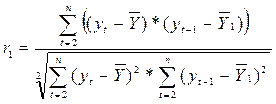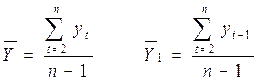 где

Расчет значений, необходимых для определения коэффициента автокорреляции первого порядка проведем в таблице 31.2

Таблица 31.2