Расчет параметров линейного уравнения множественной регрессии (по данным о деятельности крупнейших кампаний), страница 4

  Экзогенные переменные - это предопределенные переменные, влияющие на эндогенные переменные, но не зависящие от них.

  Предопределенные переменные - это экзогенные и лаговые переменные.

  В модели содержатся четыре эндогенных переменных: С_t, J_t, T_t, G_t и две предопределенных переменная: Y_t-1 и Y_t.

  Переменная G_t задана тождеством, поэтому на идентификацию необходимо проверить только три первых уравнения системы. Хотя само тождество не требует проверки на идентификацию, так как коэффициенты при переменных в тождестве известны, в проверке на идентификацию собственно структурных уравнений системы тождества участвуют.

  Пусть Н - число эндогенных переменных в j-ом уравнении;

D - число предопределенных переменных (экзогенных и лаговых), которые содержатся в системе, но не входят в j-ое уравнение.

  Тогда необходимое условие идентифицируемости системы может

быть записано в виде следующего счетного правила:

D+1=H - уравнение идентифицируемо;

D+1<H - уравнение неидентифицируемо;

D+1>H - уравнение сверхидентифицируемо.

  Достаточное условие идентификации уравнения: если  из коэффициентов,  при отсутствующих в уравнении переменных (эндогенных и экзогенных) можно получить матрицу, определить которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных без одного, то уравнение является идентифицируемым.

   Проверим выполнение необходимого условия идентификации для первого уравнения

Количество эндогенных переменных в первом уравнении равно двум (С_t и J_t): Н=2

Число отсутствующих в первом уравнении предопределенных переменных

равно единице (Y_t-1):

D=1

D+1=1+1=2=H, следовательно, необходимое условие идентификации для первого уравнения системы выполняется.

   Проверим выполнение достаточного условия идентификации для первого уравнения

   В первом уравнении отсутствуют следующие переменные: Т_t,G_t и Y_t-1

Составим матрицу из коэффициентов при этих переменных, находящихся в других уравнения системы (2-ом, 3-м  и 4-м):

Уравнения	Переменные
	Тt	Gt	Yt-1
2-ое	0	0	b21
3-е	-1	0	0
4-е	0	-1	0

det(A)=0*0*0+(-1)*(-1)*b₂₁+0*0*0-0*0*b₂₁-0*(-1)*0-0*(-1)*0=b₂₁¹0

Ранг матрицы равен трем, т.е. равен числу эндогенных переменных системы без 1, следовательно, достаточное условие идентификации выполняется, и первое уравнение является точно идентифицируемым.

Проверим выполнение необходимого условия идентификации для второго уравнения.

Количество эндогенных переменных во втором уравнении равно одному (J_t): Н=1

Число отсутствующих во втором уравнении предопределенных переменных равно 1 (Y_t)

D=1

D+1=1+1=2>H=1, следовательно, второе уравнения системы в соответствии со счетным правилом является сверхидентифицированным.

   Проверим выполнение достаточного условия идентификации для второго уравнения

   Во втором уравнении отсутствуют переменные: С_t, Y_t, T_t и G_t.

Составим матрицу из коэффициентов при этой переменной, находящихся в других уравнения системы (1-ом, 3-м и 4-ом):

Уравнения	Переменные
	Сt	Yt	Тt	Gt
1-ое	-1	b11	0	0
3-е	0	b31	-1	0
4-е	1	1	0	-1

Ранг матрицы равен трем, т.е. равен числу эндогенных переменных системы без 1, так как определитель квадратной подматрицы 3х3 этой матрицы не равен нулю:

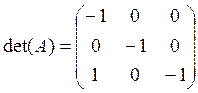=(-1)*(-1)*(-1)+0*0*0+0*0*1-1*(-1)*0-(-1)*0*0-

-0*0*(-1)=-1¹0

Таким образом, достаточное условие идентификации для второго уравнения выполняется, следовательно, второе уравнение системы является сверхидентифицированным.

   Проверим выполнение необходимого условия идентификации для третьего уравнения.

Количество эндогенных переменных в третьем уравнении равно одному (Т_t): Н=1

Число отсутствующих в третьем уравнении предопределенных переменных  равно одному (Y_t-1): D=1

D+1=1+1=2>H=1, следовательно, третье уравнения системы в соответствии со счетным правилом является сверхидентифицированным.