Особенности обобщения на математическом материале, страница 10

Попробуем построить математическую модель таких троек чисел.

                                    Þ                                            (4)

Возникают ассоциации с уравнением единичной окружности с центром в точке (0;0) , где ,  - рациональные числа.                            (5)

То есть исходная задача сводится к решению уравнения (5) в рациональных числах.

Уравнение (5) задает окружность S радиуса 1 с центром в начале координат (рис. 1).

 

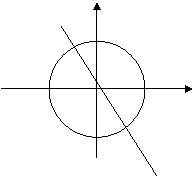
Рис. 1

Исходная задача свелась к следующей: перечислить все точки окружности с рациональными координатами. Найдем эти точки на окружности методом секущих.

Выберем одну из рациональных точек (например, точку А=(0;1)). Проведем через эту точку всевозможные прямые. Каждая такая прямая l (кроме прямой параллельной оси Ox) пересечет окружность в некоторой точке B=(x;y) и ось абсцисс в некоторой точке С=(с;0).

Сопоставляя точке В точку С мы установим взаимнооднозначное соответствие между точками окружности S (кроме точки А) и точками прямой y=0. Причем точка В будет иметь рациональные координаты тогда и только тогда, когда рациональным будет число с. Это следует из двух следующих утверждений: «если координаты двух точек рациональны, то уравнение соединяющей их прямой можно записать так, чтобы оно имело рациональные коэффициенты» и «если две прямые задаются уравнениями с рациональными коэффициентами, то точка их пересечения имеет рациональные коэффициенты».

Найдем точку пересечение прямой АС с окружностью S. Прямая, проходящая через точки А и С, определяется уравнением . Подставим его в уравнение окружности, получим:

 то есть .

Откуда  (соответствует точке А) или .                         (6)

Если число с рационально, то x и y тоже рациональны. Таким образом, каждое рациональное решение уравнения (5) получается, если в формулы (6) подставить вместо с некоторое рациональное число.

Представим число с в виде некоторой несократимой дроби , где m и n – натуральные числа. Тогда                                                   (7)

Соотнося равенства (7) и (5), получаем общие формулы пифагоровых чисел:

                          , где .

Анализ второго способа рассуждения

В ходе рассуждения была построена и проанализирована модель объекта. Построение модели позволило раскрыть внутреннюю природу исследуемого объекта. Полученные знания носят всеобщий характер, а использованную модель можно использовать как средство для решения других задач.

Таким образом, можно выделить еще один тип обобщения – обобщение через построение модели.

Вывод формулы квадрата суммы

Известна формула квадрата суммы двух переменных: . Можно поставить задачу обобщения и вывести формулу для нахождения квадрата суммы нескольких переменных.

Общая формула квадрата суммы:

.

Первый способ построения рассуждения

Найдем формулу для нахождения квадрата суммы трех слагаемых обычным раскрытием скобок: