7. Несобственные интегралы
Рассмотрим так называемые несобственные интегралы, т.е. определенный интеграл от непрерывной функции, но с бесконечным промежутком интегрирования (несобственный интеграл I рода), или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв (несобственный интеграл II рода).
Рассмотрим, как вычисляются несобственные интегралы I рода. Здесь возможны три варианта:
1) Пусть функция ![]() непрерывна
на промежутке
непрерывна
на промежутке ![]() , тогда
, тогда
|
0 а х Рисунок 19 |
Если этот предел существует, то говорят, что интеграл сходится; если же предел не существует или бесконечен, то говорят, что интеграл расходится. |
2) Если функция ![]() непрерывна
на промежутке
непрерывна
на промежутке ![]() , тогда
, тогда
|
в 0 х Рисунок 20 |
Сходимость и расходимость такого интеграла определяется аналогично. |
Несобственный интеграл с двумя бесконечными пределами интегрирования определяется формулой
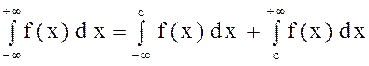 ,
,
где с – произвольное число.
|
у
0 с х Рисунок 21 |
Интеграл, стоящий в левой части равенства, сходится лишь тогда, когда сходятся оба интеграла, стоящие в правой части равенства. |
Вычислить несобственные интегралы или установить их расходимость :
1. 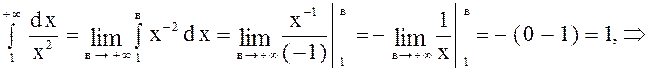 данный интеграл
сходится.
данный интеграл
сходится.
2. 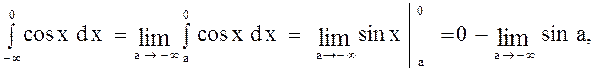 т. к. при
т. к. при ![]()
![]() не существует,
не существует, ![]() данный интеграл расходится.
данный интеграл расходится.
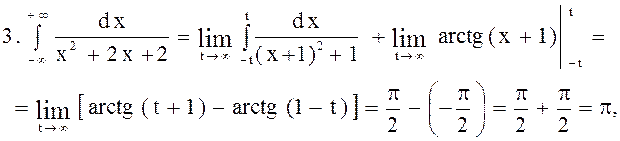
следовательно, данный интеграл сходится.
В некоторых задачах нет необходимости вычислять интеграл, достаточно лишь знать, сходится он или нет.
Сформулируем признак сходимости:
Интеграл 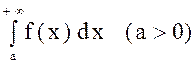 : 1) сходится, если
: 1) сходится, если 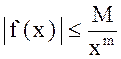 и
и ![]() ;
;
2) расходится, если 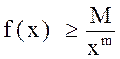 и
и
![]() , где М, m - постоянные.
, где М, m - постоянные.
Пример.
Установить, сходится или расходится интеграл 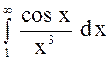 ,
используя признак сходимости.
,
используя признак сходимости.
Решение. Так как ![]() , то
, то 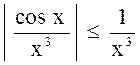 , т.е. подынтегральная функция
удовлетворяет условию (1) при
, т.е. подынтегральная функция
удовлетворяет условию (1) при ![]() ,
, ![]() данный интеграл сходится.
данный интеграл сходится.
Теперь рассмотрим, как вычисляются несобственные интегралы II рода.
Если функция ![]() терпит бесконечный
разрыв в точках
терпит бесконечный
разрыв в точках ![]() , или
, или ![]() ,
или
,
или ![]() , то интеграл
, то интеграл 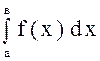 называется
несобственным интегралом II рода.
называется
несобственным интегралом II рода.
Таким образом, при вычислении таких интегралов также возможны три варианта:
|
0 а Рисунок 22 |
1)
если
|
|
0 а Рисунок 23 |
2)
если
|
||||||||||||
|
0 а Рисунок 24 |
3)
если
|
||||||||||||
Если хотя бы один из пределов не существует или равен бесконечности, несобственный интеграл II рода расходится. В противном случае – сходится.
Вычислить несобственные интегралы или установить их расходимость:
1. 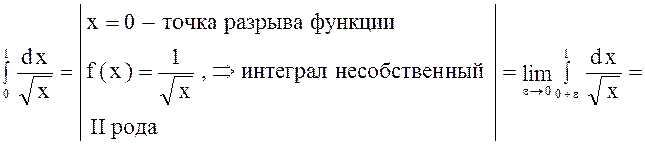
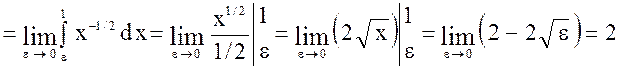 ,
,
следовательно, данный интеграл сходится.
2. 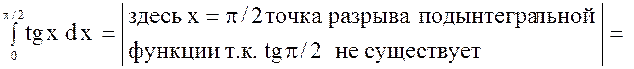
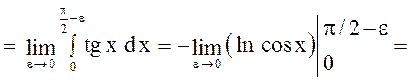
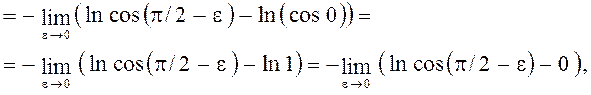
так как этот предел не существует, следовательно, данный интеграл расходится.
3. 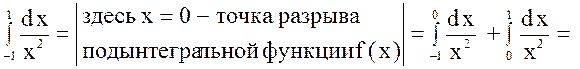
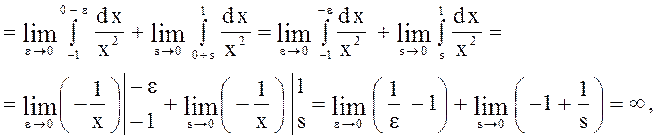
следовательно,
данный интеграл расходится ![]() .
.
Задания для самостоятельной работы
Вычислить несобственные интегралы или установить их расходимость:
Ответы:
|
1.
|
|
|
2.
|
1. |
|
3.
|
Расходится. |
|
4.
|
6. |
|
5.
|
1. |
|
6.
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.