|
|
а) Построим графики данных функций:
|
![]() ;
;
![]() откуда координаты вершины
откуда координаты вершины ![]() , ветви вниз. Находим точки пересечения
параболы с осью
, ветви вниз. Находим точки пересечения
параболы с осью ![]() :
:
![]() ,
, ![]() ,
, ![]() или
или ![]() ,
, ![]() .
.
б) Чтобы найти площадь данной фигуры, разобьем ее на части. Для этого найдем координаты точек пересечения графиков, решив систему уравнений данных линий:
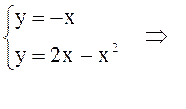
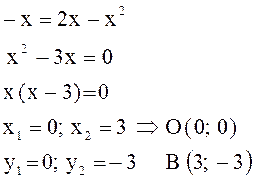
Тогда
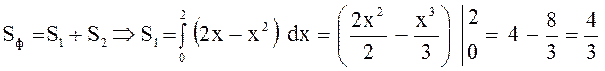 (кв. ед).
(кв. ед).
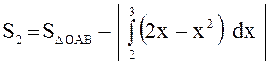 ;
; 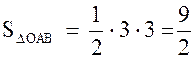 (кв.
ед.).
(кв.
ед.).
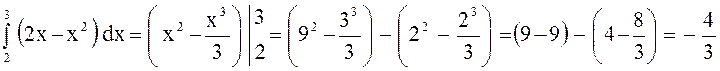 .
.
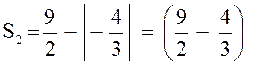 (кв. ед).
(кв. ед).
в) 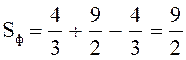 (кв. ед.)
(кв. ед.)
Замечание. Площадь этой же фигуры можно вычислить более рациональным способом, применив формулу
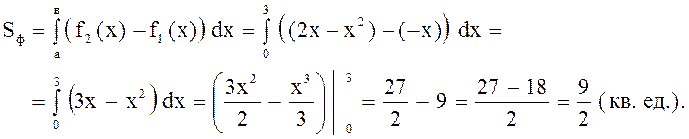
Ответ: ![]() кв. ед.
кв. ед.
Пример 2.
Вычислить площадь фигуры, ограниченной кривой ![]() , прямой
, прямой
![]() и осью Оу.
и осью Оу.
Решение.
|
1 0 1 -1 Рисунок 10 |
а) Построим графики данных функций;
|
б) Для вычисления площади этой фигуры воспользуемся
случаем, когда кривая задана функциональной зависимостью ![]() . Выразим
. Выразим ![]() через
через
![]() :
:
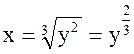 .
.
Тогда 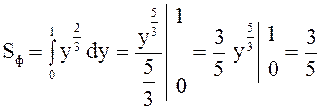 (кв.
ед.).
(кв.
ед.).
Ответ: 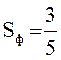 кв. ед.
кв. ед.
Замечание. Если линия, ограничивающая криволинейную трапецию, задана параметрически, то
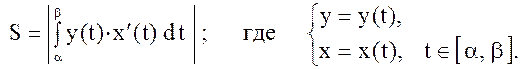
Пример 3.
Вычислить площадь фигуры, ограниченной линиями: 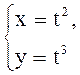 ,
прямой
,
прямой ![]() и осью
и осью ![]() .
.
Решение.
Построим графики данных функций. Так как одна из линий задана параметрически, то придавая параметру произвольные значения, составим таблицу значений функции.
1
0 1 -1 |
Таким образом, считая
(
в нашем случае
(
в нашем случае Тогда
|
||||||||||||||||||
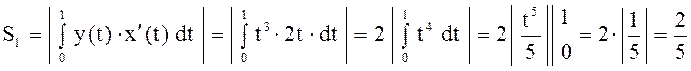 (кв. ед.).
(кв. ед.).
![]() кв. ед.
кв. ед.
Ответ:
![]() кв. ед.
кв. ед.
2. Вычисление площадей плоских фигур в случае, когда линии, их ограничивающие, заданы в полярной системе координат.
Если непрерывная кривая задана в полярных координатах
уравнением ![]() , то площадь сектора АОВ вычисляется по
формуле:
, то площадь сектора АОВ вычисляется по
формуле:
|
А
0 Рисунок 11 |
|
Пример
4. В полярной системе координат
построить фигуру, ограниченную указанной линией, и вычислить ее площадь: ![]() .
.
Решение.
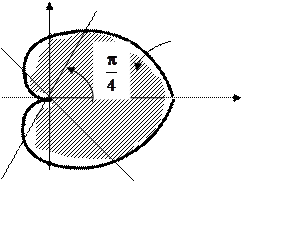
а)
Составим таблицу значений ![]() задавая шаг для
задавая шаг для ![]() .
.
|
2 0,6
0 4 0,6 Рисунок 12 График этой функции – кардиоида. |
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.