Определение определенного интеграла. Основные свойства определенного интеграла. Приложения определенного интеграла, страница 5

При вращении данной плоской фигуры вокруг оси Оу образуется тело с «вырезанным» круговым цилиндром, получающимся при вращении прямоугольника ОВСF вокруг Оу, причем он состоит из двух цилиндров с объемами . Найдем объем тела, полученного при вращении криволинейной трапеции АВСD вокруг Оу:

4  В  С                                       А   К                                Д           0       F                             Е       х

Тогда  (куб. ед.).

Ответ:   куб. ед.

 4. Площади поверхностей, образованных вращением

дуги кривой вокруг оси Ох

а) Если кривая задана уравнением вида:  , то

                            .

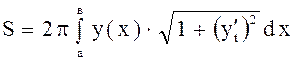б) Если кривая задана параметрическими уравнениями: 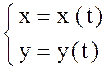 , причем  ,  , то

                          ,

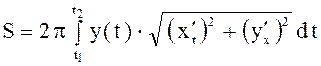где   - значения параметра  , соответствующие концам дуги.

в) Если кривая задана уравнением в полярных координатах , где   и    имеет непрерывную  производную  на  , то

                          .

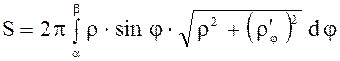Рассмотрим примеры.

Пример 1. Найти площадь поверхности, образованной вращением полуокружности, расположенной выше оси Ох, вокруг нее.

Решение.

у                                   R                 В                       А               -R          0         R            x

а) уравнение  окружности   ,   ,       ,   т.  к. окружность расположена выше оси Ох,   ;

   .

 

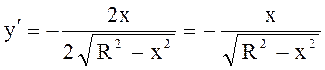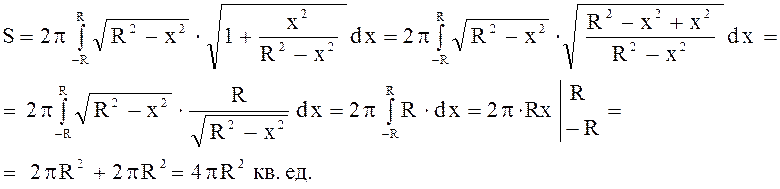
б)  Найти площадь той же  поверхности, если  кривая  задана  параметрически.

Решение. 

Уравнение данной окружности, заданной в параметрической виде: 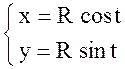,   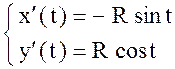 , найдем значения параметра, считая концами дуги точки  ,  подставим абсциссы этих точек в уравнение для  х: т. е.  , тогда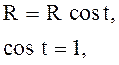   

Найдем аналогично   :    

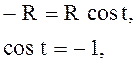
Тогда по формуле:

               

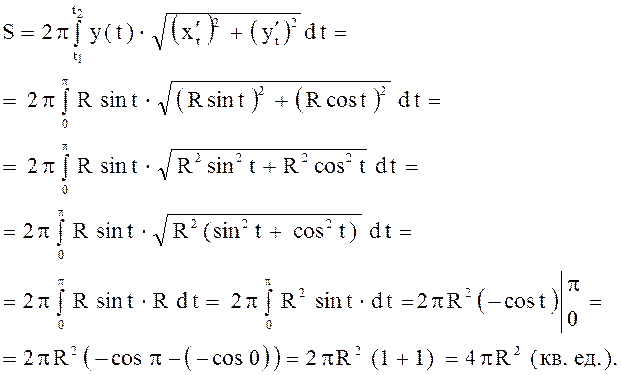
в)  Найти площадь той же поверхности, если кривая задана в полярной системе координат.

Решение. В полярной системе координат уравнение данной окружности имеет вид: , т. к.  уравнение окружности в прямоугольных координатах , тогда по формулам перехода в полярную систему координат: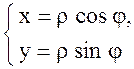         

                           

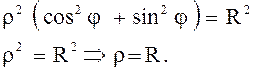
Так как  ,  найдем площадь данной поверхности:

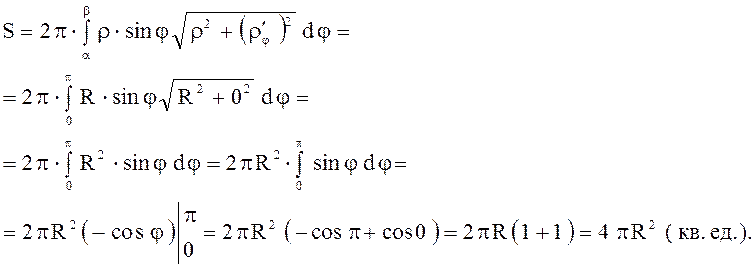
Задания для самостоятельной работы

I. Вычислить объемы тел, образованных вращением фигуры, ограниченной линиями:

                                                                                                    Ответы:

1.   где  вокруг       а) оси Ох;   б)  оси Оу.	а)  ( ед.3 ). б)   ( ед.3 ).
2.    и осью  Оу вокруг оси Оу.	( ед.3 ).
3.  и биссектрисой I  координатного угла вокруг оси Ох.	( ед.3 ).

       II. Вычислить площади поверхностей, полученных вращением кривых вокруг оси Ох.

1.  ;	(кв. ед.).
2.  ,    ;	(кв. ед.).
3.    вокруг полярной оси.	(кв. ед.).

5. Приложения определенных интегралов к решению

физических задач

1)  Путь, пройденный точкой.

Пусть точка движется по некоторой кривой и абсолютная величина скорости ее  есть известная функция времени  . Тогда путь, пройденный точкой  за  промежуток времени  , равен:  .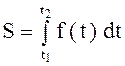

Пример.

Скорость тела задается формулой  м/с. Найти путь, пройденный те-

лом за первые  10 секунд после начала движения.

Решение.

Здесь  , тогда

           

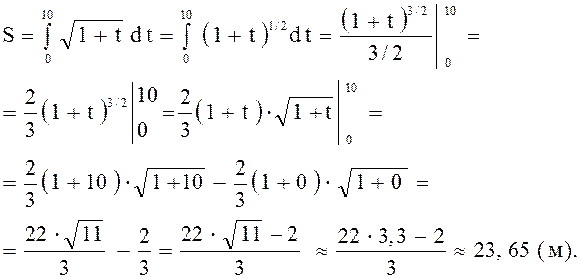
Ответ: 

2) Работа силы.

Если переменная сила  действует в направлении оси Ох, то работа силы на отрезке   равна  .

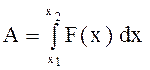Пример. Какую работу нужно затратить, чтобы растянуть пружину на  0,06 м,  если сила 1 Н растягивает ее на 0,01 м ?

Решение.

Так как , где   - коэффициент пропорциональности,   - сила, растягивающая пружину на  м.

Полагая 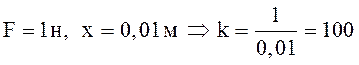;  , тогда

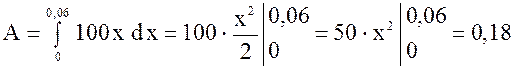  (дж).

Ответ:   дж.

3) Статические моменты и центр тяжести плоской фигуры.

А               В                     0            а                в        х                        Рисунок 16

Пусть дана материальная плоская фигура (пластинка), ограниченная кривой  и прямыми: (осью Ох),  (см. рис. 16). Считаем, что поверхностная плотность пластинки постоянная, т.е. . Тогда масса всей пластинки находится по формуле:                     .