Рассмотрим применение этой формулы на примерах:
![]()
![]()
![]()
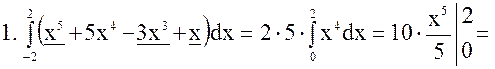
нечетные функции, ![]() интегралы
от них =0. =
интегралы
от них =0. =
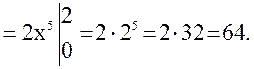
![]()
|
|
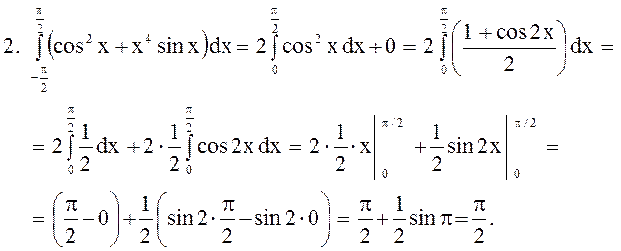
II. Основные свойства определенного интеграла
1. 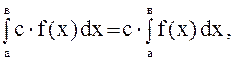
где
![]() .
.
2.
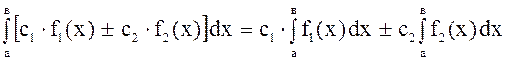 ;
;
где ![]() .
.
3. 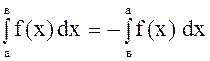 .
.
4. 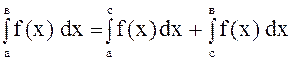 ,
,
если
![]() .
.
5. Если ![]() сохраняет знак на
отрезке
сохраняет знак на
отрезке ![]() , то интеграл
, то интеграл 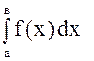
сохраняет
тот же знак, т. е. например, если ![]() для любого
для любого 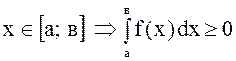 .
.
6. Если ![]() - непрерывна на отрезке
- непрерывна на отрезке
![]() , то существует такая точка
, то существует такая точка ![]() , что
, что 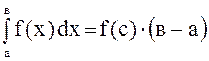 (теорема
«о среднем»).
(теорема
«о среднем»).
7. Если ![]() при
при ![]() , то
, то 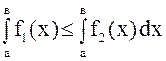 .
.
8. Если ![]() - наименьшее, а
- наименьшее, а ![]() - наибольшее значения функции
- наибольшее значения функции ![]() непрерывной на отрезке
непрерывной на отрезке ![]() , то:
, то:
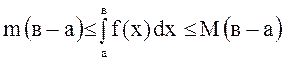 (теорема
«об оценке»).
(теорема
«об оценке»).
9. 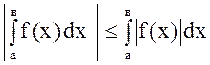 , где
, где ![]() .
.
Пример 1. Вычислить
среднее значение функции 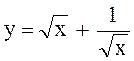 на отрезке
на отрезке ![]() .
.
Решение. Так
как ![]() является непрерывной на указанном отрезке,
то можно применить свойство 6 (теорему о среднем);
является непрерывной на указанном отрезке,
то можно применить свойство 6 (теорему о среднем);
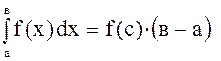 выразим
выразим ![]() из данного соотношения как неизвестное из
уравнения:
из данного соотношения как неизвестное из
уравнения:
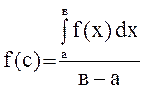 , т. е.
, т. е.
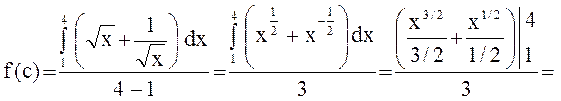
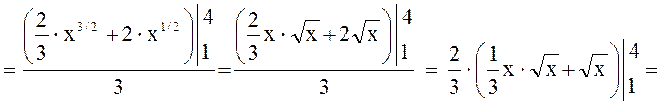
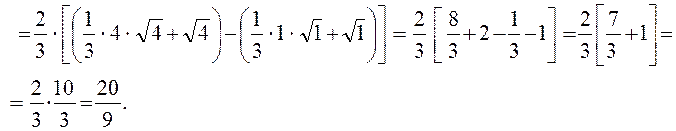
Пример
2. Оценить интеграл: 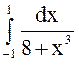 .
.
Применим теорему «об оценке» определенного интеграла (свойство 8).
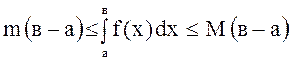 .
.
Найдем значения функции на концах отрезка:
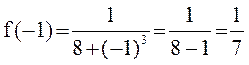 ,
, 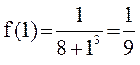 .
.
Найдем
также ![]() . Так как здесь
. Так как здесь ![]() -
наименьшее значение, а
-
наименьшее значение, а
![]() - наибольшее значение
функции,
- наибольшее значение
функции, ![]()
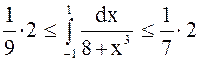 .
.
Ответ: 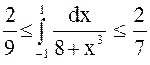 .
.
Пример 3. Не
вычисляя, сравнить значения интегралов: 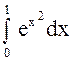 или
или
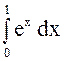 .
.
Решение. Так как ![]() при
при ![]() по свойству 7
по свойству 7 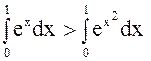 .
.
Задания для самостоятельной работы.
Вычислить определенные интегралы с помощью формулы Ньютона –Лейбница:
|
1.
|
Ответ: 66. |
|
2.
|
Ответ: 1. |
|
3.
|
Ответ: 40. |
|
4.
|
Ответ:
|
|
5.
|
Ответ:
|
|
6.
|
Ответ:
|
|
7.
|
Ответ:
|
|
8.
|
Ответ:
|
|
9.
|
Ответ:
|
|
10.
|
Ответ:
|
|
11.
|
Ответ:
|
|
12.
|
Ответ: 3. |
III. Приложения определенного интеграла
1. С помощью определенного интеграла можно вычислять площади плоских фигур, ограниченных кривыми. Напомним, что кривые могут быть заданы различными способами, т.е.
1) в прямоугольных декартовых координатах (в явном виде и параметрически);
2) в полярных координатах.
Рассмотрим случаи вычисления площадей плоских фигур в прямоугольных координатах.
а) если фигура представляет из себя криволинейную трапецию вида.
![]()
|
Рисунок 5 |
|
б) если криволинейная трапеция расположена ниже оси ![]() , т.е.
, т.е. ![]() тогда
исходя из свойств определенного интеграла
тогда
исходя из свойств определенного интеграла
|
Рисунок 6 |
|
В общем случае 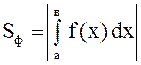 ;
;
в) если плоская фигура имеет сложную форму, т.е.
прямые ![]() «вырождаются» в точки, то фигуру следует
разбить на части так, чтобы можно было применить известные формулы.
«вырождаются» в точки, то фигуру следует
разбить на части так, чтобы можно было применить известные формулы.
Проиллюстрируем некоторые возможные варианты:
|
Рисунок 7 |
|
|
г)
Рисунок 8 |
|
д) если криволинейная трапеция ограничена прямыми ![]() и
и
![]() , осью
, осью ![]() и
непрерывной кривой
и
непрерывной кривой ![]() , то
, то ![]()
|
Рисунок 9 |
|
Рассмотрим примеры нахождения площади плоских фигур:
Пример 1.
Найти площадь фигуры, ограниченной линиями: 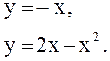
Решение.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.