Определение определенного интеграла. Основные свойства определенного интеграла. Приложения определенного интеграла, страница 6

Статические моменты относительно координатных осей  Ох   и  Оу  находятся по формулам:

                      ;         .

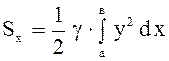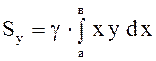А координаты  центра тяжести  С  этой пластинки вычисляются по формулам:

                           .

Пример.

Найти статические моменты относительно осей  Ох   и  Оу  и координаты центра тяжести треугольника, ограниченного прямыми  , (плотность ).

Решение.

у     а                                                 а/3            С                   0        а/3          а               х

Вычислим массу данной пластинки:

          

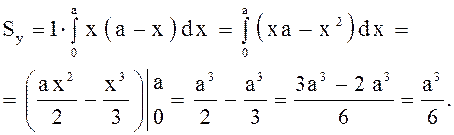
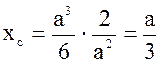, аналогично .

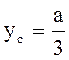Ответ: .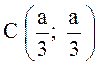

4) Количество электричества.

Пусть по проводнику течет ток переменной силы  , где  . Тогда количество электричества Q , протекшего через поперечное сечение проводника за промежуток времени , вычисляется по формуле:

                                  ,

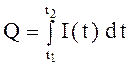где  I  - выражено в амперах;   t – в секундах.

Рассмотрим пример.

Сила тока  I  в проводнике меняется со временем по закону  . Определить, какое количество электричества проходит через поперечное сечение проводника за время от

Решение.

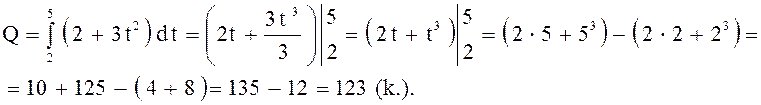
Ответ:  .

6. Приближенное вычисление определенных интегралов

На практике часто требуется вычислить определенные интегралы от функций, для которых не удается найти первообразные. В этом случае осуществляют численный расчет по формулам приближенного интегрирования. Иногда это удобно делать и для функций, первообразные которых найти можно.

Рассмотрим три наиболее употребляемые формулы вычисления определенного интеграла – формулу прямоугольников, формулу трапеций и формулу парабол (Симпсона).

Пусть необходимо вычислить интеграл 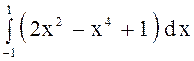 , пользуясь этими формулами. Построим график данной функции на заданном отрезке.

у                     2                                        1               - 1      0        1               х                   Рисунок 17

1) Так как первообразную этой  функции найти легко, вначале вычислим этот интеграл, пользуясь формулой Ньютона – Лейбница.

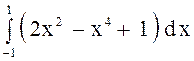 =  т. к. пределы интегрирования симметричны, а подынтегральная функция четная, воспользуемся свойством интегрирования четных функция в симметричных отрезках   =

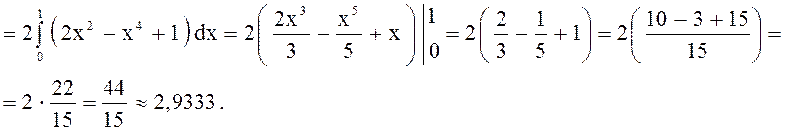
2)  Рассмотрим на этом же примере метод прямоугольников.

Рисунок 18

Отрезок  разбивается на    равных  частей  длины                  . В середине    каждого такого отрезка строим ординату . Приняв эту ординату за высоту, построим прямоугольник с площадью . Тогда сумма площадей всех    прямоугольников дает площадь фигуры, представляющую собой

приближенное значение искомого определенного интеграла:

          ,

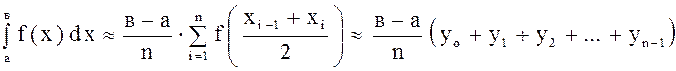где  .

Нашу фигуру мы разбили на 8 равных частей с шагом

                   .

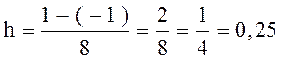Тогда при:

,

,

,

,

,

,

,

 ,

.

Подставляем найденные значения в формулу:

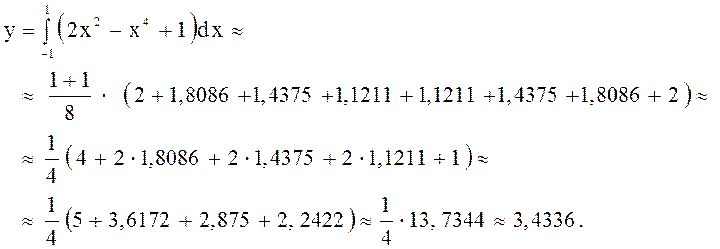
2)  Теперь рассмотрим метод трапеций для этого же интеграла.

Эту формулу получают аналогично предыдущей, достраивая в процессе разбиения каждую фигуру до обычной трапеции.

Тогда

             

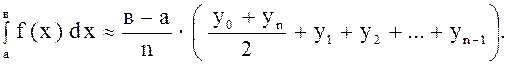
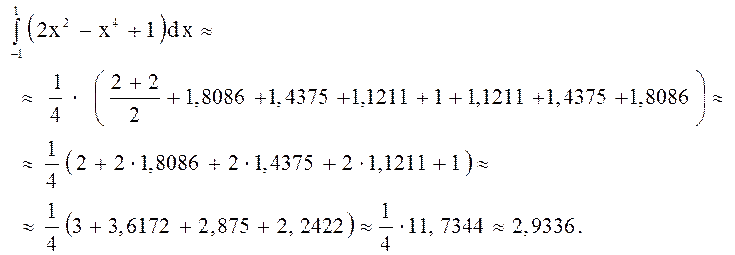
3)  Вычислим данный интеграл по формуле парабол (формула Симпсона).

Если  заменить график функции на каждом отрезке разбиения не отрезками прямых, а дугами парабол, то получим формулу Симпсона:

               

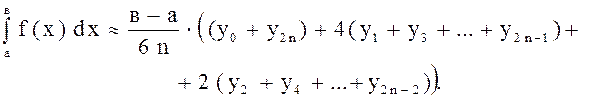
В нашем случае: т.к. отрезок разбивается на    равных частей, то

            

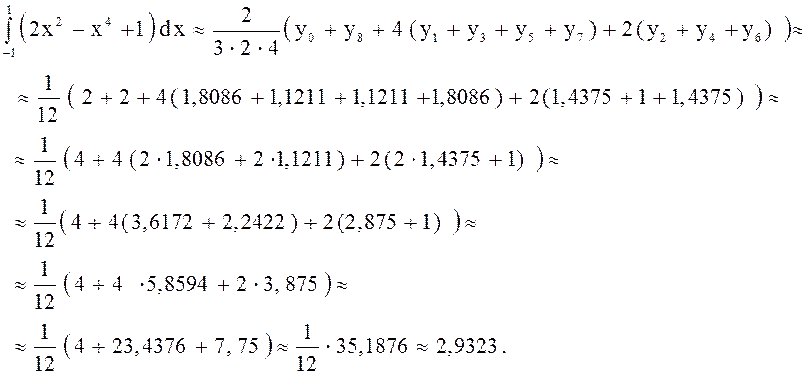
      Вывод. Сравнивая ответы, видим, что данный интеграл приближенно находится с различной степенью точности по различным формулам.

Задания для самостоятельной работы

Вычислить приближенно определенные интегралы:

                                                                                                                      Ответы:

1.  , разбивая отрезок [ 1; 2 ] на 10 частей с округлением до 4-го       десятичного знака по формуле   прямоугольников.	0, 7188
2.  ,  разбивая отрезок  [ 0; 1 ] на 6 частей с округлением       до 4-го десятичного знака по формуле трапеций.	0, 8109
3.  , разбивая отрезок [ 1; 3] на 4 части с округлением до 4-го      десятичного знака по формуле Симпсона.	0, 8111