|
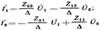
Обозначим
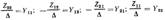
и перепишем уравнения четырехполюсника, решенные
относительно токов, в виде:
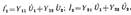
где Y11 - входная
проводимость четырехполюсника, измеренная на входе при закороченном выходе;
Y 22 - входная
проводимость, измеренная на выходе при закороченном входе;
Y12 и Y 21 - проводимости передачи, измеренные при закороченных
входах.
Для обратимого 4-хполюсника Y12=Y21. Входные
проводимости короткого замыкания Y11 и Y22
симметричного четырехполюсника равны.
У обратимого симметричного четырехполюсника независимы
два параметра: входная проводимость и проводимость передачи. Остальные находятся
из условий: Y12=Y21, Y11=Y22.
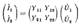
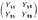 - называют матрицей проводимостей короткого замыкания
четырехполюсника. - называют матрицей проводимостей короткого замыкания
четырехполюсника.
|
В устройствах автоматики,
телемеханики и связи часто возникает задача выделения полезных сигналов из
смеси различных сигналов и помех. Если полезные сигналы и помехи различаются
занимаемыми частотными полосами, то такое разделение осуществляют частотными
электрическими фильтрами. Частотные фильтры, отделяющие электрические
колебания токов с одними частотами от колебаний с другими частотами,
применяют в самых разнообразных частотных диапазонах. Простейшими фильтрами
могут служить цепи rCили реактивные двухполюсники. Однако наиболее
распространены фильтры, представляющие собой четырехполюсники, составленные
из реактивных двухполюсников по цепочечным или мостовым схемам. Эти фильтры
отличаются от простейших фильтрующих цепей более качественными частотными
характеристиками. По сравнению с используемыми в качестве фильтров цепями rС они имеют в полосе пропускания теоретически нулевое, а практически
весьма малое затухание. От активных фильтров rС их
выгодно отличает возможность работы при больших токах, например, в цепях
тяговых сетей и рельсовых цепях. В то же время фильтры LCимеют
и недостатки: невысокую добротность элементов (особенно катушек
индуктивности) и значительные габаритные размеры, что затрудняет их
использование на сверхнизких и высоких частотах.
Учет влияния сопротивления
нагрузки фильтра требует полного анализа его свойств как четырехполюсника.
Последнее может быть осуществлено использованием любого полного набора
параметров четырехполюсника.
Для анализа и синтеза
реактивных фильтров наиболее удобно использовать собственные параметры
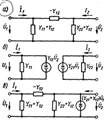
передачи g и Zx. Цепочечные
фильтры представляют собой каскадное соединение Г-, Т- или П-образных
четырехполюсников, содержащих реактивные сопротивления.
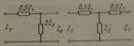

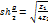 Это выражение справедливо для Т- и
П-образных четырехполюсников Для Г-образного полузвена постоянная передачи
в 2 раза
меньше. Из определения электрического фильтра следует, что его
затухание в полосе пропускания должно быть минимальным (теоретически равняться
нулю), а в полосе задерживания зависеть от частоты (быть максимальным). С
учетом этого условия пропускания и задерживания цепочечных фильтров можно
получить, анализируя зависимость постоянной передачи цепочечных схем от
параметров схемы в широком диапазоне частот. Напомним, что собственная
постоянная передачи g= а + jbопределяет затухание и фазовый сдвиг четырехполюсника в
условиях согласованной нагрузки (Zn = Zx). Проанализируем
выражение Это выражение справедливо для Т- и
П-образных четырехполюсников Для Г-образного полузвена постоянная передачи
в 2 раза
меньше. Из определения электрического фильтра следует, что его
затухание в полосе пропускания должно быть минимальным (теоретически равняться
нулю), а в полосе задерживания зависеть от частоты (быть максимальным). С
учетом этого условия пропускания и задерживания цепочечных фильтров можно
получить, анализируя зависимость постоянной передачи цепочечных схем от
параметров схемы в широком диапазоне частот. Напомним, что собственная
постоянная передачи g= а + jbопределяет затухание и фазовый сдвиг четырехполюсника в
условиях согласованной нагрузки (Zn = Zx). Проанализируем
выражение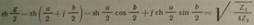 (1.1) (1.1)
При чисто реактивном
характере сопротивлений Zxи Z2
возможны два варианта их соотношений.
Вариант 1. Величины Z1и Z2 — реактивные сопротивления одного знака, в этом случае 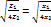 положительное вещественное число, не
зависящее от частоты. положительное вещественное число, не
зависящее от частоты.
Тогда из равенства (1.1)
получим два уравнения:
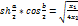 ; ; 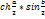 =0 (1.2) =0 (1.2)
Так как 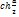 не может быть равным нулю, то из
уравнений (1.2) следует
что не может быть равным нулю, то из
уравнений (1.2) следует
что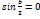 , при этом , при этом 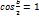 , а , а 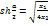 (1.3) (1.3)
Таким образом,
четырехполюсники, сопротивления Z1и Z2 которых имеют одинаковые реактивные знаки во всем диапизоне
частот не могут быть фильтрами, поскольку их затухание является постоянной не
зависящей от частоты величиной.Это обычные делители напряжения.
Вариант 2. Величины Z1и Z2 - реактивные сопротивления различных знаков, тогда
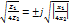 -мнимое число, не зависящее от
частоты. В этом случае равенство (1.1) распадается на два уравнения: -мнимое число, не зависящее от
частоты. В этом случае равенство (1.1) распадается на два уравнения: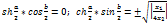 (1.4) (1.4)
Система уравнений (1.4)
допускает два решения
Первое решение: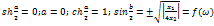 (1.5) (1.5)
Второе решение: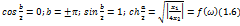 Здесь возможны два режима: режим пропускания,
соответствующий первому решению, когда затухание а = 0, и режим
задерживания, соответствующий второму решению, когда а ≠0.
Следовательно, четырехполюсник цепочечной схемы, образованный из реактивных
сопротивлений Z1и Z2 разных знаков, является электрическим фильтром. Здесь возможны два режима: режим пропускания,
соответствующий первому решению, когда затухание а = 0, и режим
задерживания, соответствующий второму решению, когда а ≠0.
Следовательно, четырехполюсник цепочечной схемы, образованный из реактивных
сопротивлений Z1и Z2 разных знаков, является электрическим фильтром.
|
Виды аппроксимации.
Функция передачи ФНЧ в
общем случае может быть представлена в виде 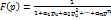 (1.1) Чем выше порядок
фильтра n, тем больше элементов в его схеме и более резко осуществляется
переход от полосы пропускания к полосе задерживания. Однако ни одна реальная
схема, содержащая конечное число элементов, не может дать желательной хар-ки.
И таким образом встает задача приближения указанной зависимости к функции
вида (1.1) - задача аппроксимации. При расчете фильтров в
завис-ти от конкретных требований, предъявляемых к нему со стороны системы,
эл-ом кот. он является, примен. несколько видов приближения фун-ии передачи
фильтра к идеальной. Виды аппроксимации: максимально плоская,
равноволновая, обратная чебышевская, эллиптическая. Максимально
плоская аппроксимация (Баттерворта). При использова-нии
максимально плоской аппроксимации модуль функции передачи фильтра
аппроксимируется монотонной кривой в полосах пропускания и задерживания. Для
определения модуля фун-ии передачи фильтра следует исключить из
рассмот-рения фазочастотную хар-ку. Это можно осуществить, перейдя к формуле
(1.1) к квадрату модуля фун-ии передачи и учитывая, что pн=jΏ:
|F (1.1) Чем выше порядок
фильтра n, тем больше элементов в его схеме и более резко осуществляется
переход от полосы пропускания к полосе задерживания. Однако ни одна реальная
схема, содержащая конечное число элементов, не может дать желательной хар-ки.
И таким образом встает задача приближения указанной зависимости к функции
вида (1.1) - задача аппроксимации. При расчете фильтров в
завис-ти от конкретных требований, предъявляемых к нему со стороны системы,
эл-ом кот. он является, примен. несколько видов приближения фун-ии передачи
фильтра к идеальной. Виды аппроксимации: максимально плоская,
равноволновая, обратная чебышевская, эллиптическая. Максимально
плоская аппроксимация (Баттерворта). При использова-нии
максимально плоской аппроксимации модуль функции передачи фильтра
аппроксимируется монотонной кривой в полосах пропускания и задерживания. Для
определения модуля фун-ии передачи фильтра следует исключить из
рассмот-рения фазочастотную хар-ку. Это можно осуществить, перейдя к формуле
(1.1) к квадрату модуля фун-ии передачи и учитывая, что pн=jΏ:
|F 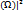 =F(jΏ)F(jΏ)= =F(jΏ)F(jΏ)=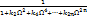 (1.2) Из выражения (1.2)
следует, что при Q < 1 младшие степени
вносят большой вклад в его знаменатель, и, следовательно, приводят к
существенному уменьшению коэффициента передачи фильтра. Поэтому для того
чтобы фун-ия передачи была максимально плоской на частотах, меньших частоты
среза, необходима зависимость фун-ии |F (Ώ)|
только от старшей степени Ώ. Равноволновая
аппроксимация (Чебышева). Эту аппроксимацию
осуществляют на основе использования полиномов Чебышева. Аппроксимирующая
фун-ия в полосе пропускания фильтра имеет колебательный хар-р с равными
отклонениями от заданной фун-ии и монотонный в области задерживания, что
опред. св-ми полиномов Чебышева. Полиномы Чебышева имеют вид: (1.2) Из выражения (1.2)
следует, что при Q < 1 младшие степени
вносят большой вклад в его знаменатель, и, следовательно, приводят к
существенному уменьшению коэффициента передачи фильтра. Поэтому для того
чтобы фун-ия передачи была максимально плоской на частотах, меньших частоты
среза, необходима зависимость фун-ии |F (Ώ)|
только от старшей степени Ώ. Равноволновая
аппроксимация (Чебышева). Эту аппроксимацию
осуществляют на основе использования полиномов Чебышева. Аппроксимирующая
фун-ия в полосе пропускания фильтра имеет колебательный хар-р с равными
отклонениями от заданной фун-ии и монотонный в области задерживания, что
опред. св-ми полиномов Чебышева. Полиномы Чебышева имеют вид: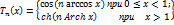 Функция Тn
(х) колеблется в пределах ±1 в интервале |х| < 1 и монотонно
возрастает при |х| > 1. алгебраическая форма полиномов Чебышева: Функция Тn
(х) колеблется в пределах ±1 в интервале |х| < 1 и монотонно
возрастает при |х| > 1. алгебраическая форма полиномов Чебышева: 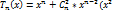 -1)+ -1)+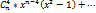 Вид полиномов Чебышева первых четырех
порядков: Вид полиномов Чебышева первых четырех
порядков:
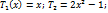
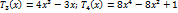
Полиномы Чебышева из всех
многочленов степени n
наименее уклоняются от нуля на отрезке - 1 <х< 1, что является важной
их особенностью. Таким образом, фильтры Чебышева характеризуются двумя параметрами
- порядком и допустимой неравномерностью затухания в полосе пропускания. Обратная
чебышевская аппроксимация. Этот вид аппроксимации характеризуется
монотонностью аппроксимирующей фун-ии в полосе пропускания и колебательным
характером в области задерживания. Квадрат модуля функции передачи при этом
имеет вид: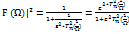 (1.6) Фун-ия передачи
монотонна в полосе пропускания фильтра (т. е. при (1.6) Фун-ия передачи
монотонна в полосе пропускания фильтра (т. е. при  < 1), если аргумент многочлена Тn (х) больше
единицы. Фильтры, модуль фун-ии передачи которых определяется выражением (1.6),
называют обратными (инверсными) фильтрами Чебышева. Фун-ия передачи таких
фильтров колеблется в области задерживания с амплитудой < 1), если аргумент многочлена Тn (х) больше
единицы. Фильтры, модуль фун-ии передачи которых определяется выражением (1.6),
называют обратными (инверсными) фильтрами Чебышева. Фун-ия передачи таких
фильтров колеблется в области задерживания с амплитудой 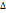 F = F = 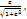 Таким образом, использование полиномов
Чебышева дает возможность получить равноволновое приближение
аппроксимирующей функции к заданной в полосе пропускания или в области
задерживания фильтра.
Эллиптическая аппроксимация.
Она позволяет добиться равноволнового хар-ра приближения аппроксимирующей
функции к заданной в полосе пропускания и вобласти задерживания
фильтра, для чего используют эллиптические функции Якоби. Выбор
того или иного вида
аппроксимирующей функции зависит от конкретных требований,
предъявляемых к фильтру со стороны системы, элементом которой он является. У
фильтров Баттерворта меньшая, чем у фильтров Чебышева или эллиптических
фильтров того же порядка, крутизна нарастания затухания в области задерживания,
однако они имеют максимально плоскую характеристику в полосе пропускания. В
тех случаях, когда можно допустить некоторую неравномерность затухания в
полосе пропускания за счет увеличения крутизны нарастания затухания в
переходной области, предпочтительны фильтры Чебышева или же эллиптические,
обладающие лучшими свойствами, чем чебышевские, однако более сложные в
реализации. Если необходимо обеспечить значительную крутизну нарастания затухания
в переходной области и плоскую хар-ку в полосе пропускания фильтра, то
используют обратные фильтры Чебышева. Таким образом, использование полиномов
Чебышева дает возможность получить равноволновое приближение
аппроксимирующей функции к заданной в полосе пропускания или в области
задерживания фильтра.
Эллиптическая аппроксимация.
Она позволяет добиться равноволнового хар-ра приближения аппроксимирующей
функции к заданной в полосе пропускания и вобласти задерживания
фильтра, для чего используют эллиптические функции Якоби. Выбор
того или иного вида
аппроксимирующей функции зависит от конкретных требований,
предъявляемых к фильтру со стороны системы, элементом которой он является. У
фильтров Баттерворта меньшая, чем у фильтров Чебышева или эллиптических
фильтров того же порядка, крутизна нарастания затухания в области задерживания,
однако они имеют максимально плоскую характеристику в полосе пропускания. В
тех случаях, когда можно допустить некоторую неравномерность затухания в
полосе пропускания за счет увеличения крутизны нарастания затухания в
переходной области, предпочтительны фильтры Чебышева или же эллиптические,
обладающие лучшими свойствами, чем чебышевские, однако более сложные в
реализации. Если необходимо обеспечить значительную крутизну нарастания затухания
в переходной области и плоскую хар-ку в полосе пропускания фильтра, то
используют обратные фильтры Чебышева.
|
Параметры линии как
четырехполюсника.Любую пассивную линейную
электрическую цепь с постоянными пар-ами и четырьмя зажимами, используемую
для передачи электрической энергии в качестве промежуточного звена, можно
рассматривать как четырехполюсник. К числу таких цепей относят однородную
уединенную электрическую линию. Уравнения линии как
четырехполюсника должны связывать четыре величины: U(0),
I (0), U(l) и I (l). Для их получения вернемся к выражениям : 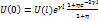 ; I(0)= ; I(0)=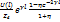 ; ;
Преобразуем выражения ,
подставив в них значение 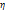 = (ZH — ZK)/
(ZH+ ZK) и
заменяя U (l)/Znна I(l). Имея в виду, что = (ZH — ZK)/
(ZH+ ZK) и
заменяя U (l)/Znна I(l). Имея в виду, что 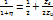 ; ; 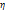 /(1+η)= /(1+η)=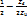 ; Получим: U(0)=U(l) ; Получим: U(0)=U(l)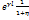 + U(l) + U(l)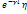 /(1+η)= U(l)ch /(1+η)= U(l)ch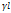 +I(l) +I(l)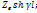
I(0)= Здесь величина Здесь величина 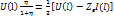 представляет coбoй
отраженную, а величина U(l) представляет coбoй
отраженную, а величина U(l)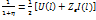 падающую волны напряжения на выходе
линии. падающую волны напряжения на выходе
линии.
Обозначим U (0) = U0; I(0) = I0; Ul(l)
= Ul ; I(l)=Il. и сопоставим уравнения
электрической линии и четырехполюсника: U(0)=Ulch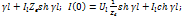
U1=AU2+BI2; I1=CU2;
Из сопоставления этих уравнений следует, что матрица пар-ров линии
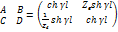 Линия как четырехполюсник симметрична,
так как A = D. Совершенно
очевидно, что уравнения линии можно представить всеми формами уравнений
четырехполюсника. Матрица проводимостей линии Линия как четырехполюсник симметрична,
так как A = D. Совершенно
очевидно, что уравнения линии можно представить всеми формами уравнений
четырехполюсника. Матрица проводимостей линии
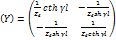 а матрица сопротивлений а матрица сопротивлений 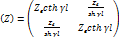

Таким образом, однородную
линию, рассматриваемую как симметричный четырехполюсник, можно
характеризовать двумя независимыми комплексными коэфф-ами, задаваемыми
различными способами: первичными пар-ами Zл, Yл, волновыми или вторичными пар-ами Zв и 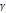 l, третичными пар-ами A,
В, С, а также матрицами проводимостей и сопротивлений. Линию
как систему передачи сигналов наиболее удобно характеризовать волновыми
параметрами: волновым сопротивлением Zв и
коэффициентом распространения l, третичными пар-ами A,
В, С, а также матрицами проводимостей и сопротивлений. Линию
как систему передачи сигналов наиболее удобно характеризовать волновыми
параметрами: волновым сопротивлением Zв и
коэффициентом распространения 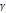 l. Волновое
сопр-ние показ., как следует подобрать сопр-ния генератора и приемника,
чтобы в линии отсутствовали отраженные волны. Коэф-ент распространения волны l. Волновое
сопр-ние показ., как следует подобрать сопр-ния генератора и приемника,
чтобы в линии отсутствовали отраженные волны. Коэф-ент распространения волны
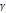 l
указ. на потери и фазовый сдвиг, возникающие при пробеге волны вдоль линии.
Величины l
указ. на потери и фазовый сдвиг, возникающие при пробеге волны вдоль линии.
Величины 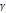 lи ZB
вполне хар-уют передающие св-ва линии при согласованной нагрузке. В
общем случае, рассматривая линию как четырехполюсник, условия передачи
энергии от генератора к приемнику можно хар-ать входным сопр-нием, сопротивлением
передачи или приведенным сопр-нием. lи ZB
вполне хар-уют передающие св-ва линии при согласованной нагрузке. В
общем случае, рассматривая линию как четырехполюсник, условия передачи
энергии от генератора к приемнику можно хар-ать входным сопр-нием, сопротивлением
передачи или приведенным сопр-нием.
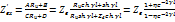 ; ;
Это выражение верно при активныхRн и комплексных Zн
сопротивлениях нагрузки.
В частныхслучаях
приRн (короткое замыкание) и Rн= ∞ (холостой ход) получим:
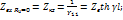 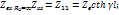 Сопротивление
передачи и приведенное сопротивление линии: Сопротивление
передачи и приведенное сопротивление линии:
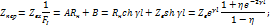
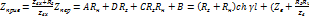 )sh )sh 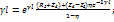 При Rг=Rн=R Zприв= При Rг=Rн=R Zприв=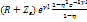 ; Можно
видеть, что наличие отраженных волн в линии в большей степени влияет на
величину Znep. и в меньшей — на ; Можно
видеть, что наличие отраженных волн в линии в большей степени влияет на
величину Znep. и в меньшей — на 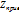 так как в последнем в числителе стоит так как в последнем в числителе стоит
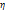 2.Использование
понятий Znep и Znpив
облегчает решение многих задач при определении напряжений и токов в линиях. 2.Использование
понятий Znep и Znpив
облегчает решение многих задач при определении напряжений и токов в линиях.
|