Задание на курсовое проектированиепо курсу «Синтез законов управления в технических системах», страница 7

.

Видно (рис.2), что ОУ имеет два апериодических полюса (апериодические звенья) и две пары комплекснo-сопряженных полюсов (колебательные звенья).

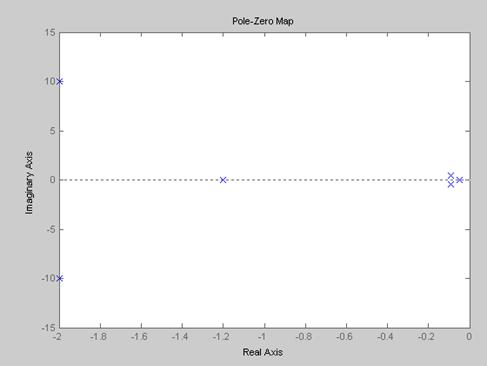
Рис.2. Карта полюсов ОУ

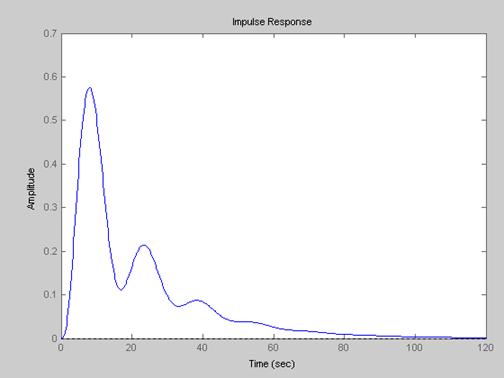
Рис.3. ИПФ ОУ

Согласно работам академика Ишлинского, динамика реального линеаризованного динамического объекта сколь угодно высокого порядка может быть приближенно описана дифференциальным уравнением второго или третьего порядка.

Действительно, вид переходного процесса в основном определяется доминирующими (самыми правыми) полюсами.

Понижение порядка объекта в данном случае производим так:

– если два самых правых полюса вещественные (два доминирующих полюса), то УОУ будет иметь второй порядок (два апериодических звена);

– если самыми правыми являются пара комплексно-сопряженных полюсов и один вещественный (три доминирующих полюса), то УОУ будет иметь третий порядок (апериодическое и колебательное звено).

При понижении порядка ОУ следует учитывать, что ПФ УОУ должна иметь коэффициент усиления, равный коэффициенту исходной ПФ.

Вернемся к примеру. Из рис.2 видно, что есть три доминирующих полюса (один вещественный и два комплексных сопряженных). Тогда ПФ УОУ имеет вид:

.

Сравнивая ИПФ исходного и упрощенного объекта (рис.3 и рис.5), наблюдаем их практическую идентичность, что свидетельствует о корректности процедуры понижения порядка.

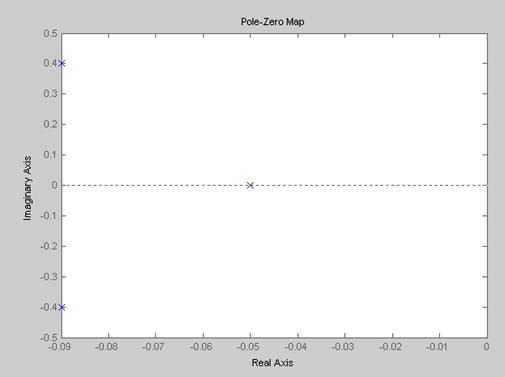
Рис.4. Карта полюсов УОУ

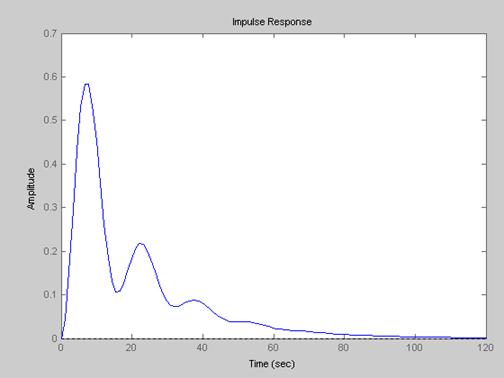
Рис.5. ИПФ УОУ

Из полюсов (простейших звеньев), невошедших в ПФ УОУ, можно сформировать ПФ части ОУ, динамика которой не будет учитываться при расчете регулятора

.

По пункту 3.

Желаемая ПФ непрерывного аналога замкнутой дискретной системы имеет вид:

,