Задание на курсовое проектированиепо курсу «Синтез законов управления в технических системах», страница 10

Определяем ДПФ  по формуле (2). Получаем:

.

В Matlab данная процедура реализуется оператором c2d( ) [2]. Период дискретизации допустимо выбирать как с. В примере с

По формуле (3) получаем:

.

Видно (рис.7), что  содержит нуль , который включаем в ДПФ :

.

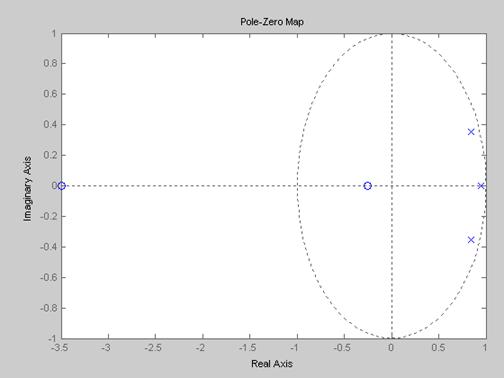
Рис.7. Карта полюсов эквивалентной ДПФ

Условие осуществимости не выполняется, так как разность степеней z знаменателя и числителя  меньше разности степеней z знаменателя и числителя . Вводим дополнительный полюс  и окончательно

.

Обратите внимание, обобщенный коэффициент усиления в последней формуле определяется по формуле:

.

Это следует из следующих формул:

;

;

,

где  – установившийся уровень на выходе дискретной системы с ДПФ  при подаче на ее вход единичного ступенчатого воздействия.

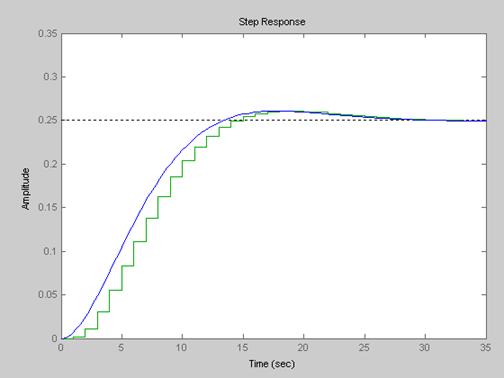
         Из рис.8 видно, что желаемый переходный процесс после корректировки  несущественно отличается от исходного.