Задание на курсовое проектированиепо курсу «Синтез законов управления в технических системах», страница 11

Рис.8. Желаемая ПХ до коррекции () и желаемая дискретная ПХ отвечающая требованиям осуществимости и грубости

По пункту 4.

ДПФ замкнутой системы определяется по формуле

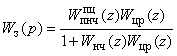                                                     ,                                                 (4)

где 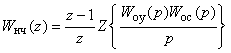 – эквивалентная ДПФ непрерывной части.

Приравнивая  к  и выражая , получаем формулу для определения ДПФ цифрового регулятора:

.

При вычислении  следует сокращать кратные нули и полюса. Если вычисления производятся в Matlab, то ПФ, фигурирующие в формуле, должны быть заданы в zpk – форме.

На рис.9 и рис.10 иллюстрируется процесс моделирования. Для примера выбрана схема моделирования с исходным ОУ и с ЦР, заданным в последовательно-декомпозированной форме. Другие схемы моделирования строятся аналогичным образом. Видно, что ЦР задается в дискретном виде, а ОУ и ЗООС в непрерывном. Период дискретизации выставляется в блоке задания ДПФ ЦР.

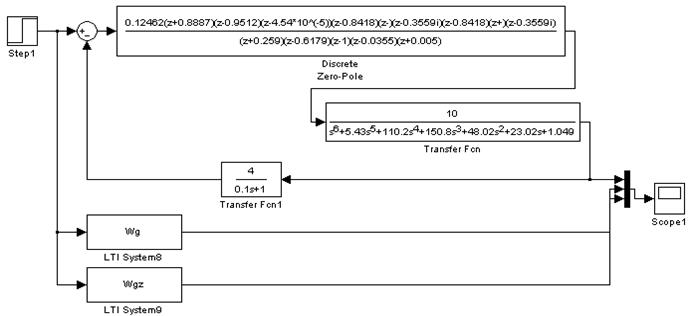
Рис.9. Схема моделирования с исходным ОУ и с ЦР, заданным в последовательно-декомпозированной форме

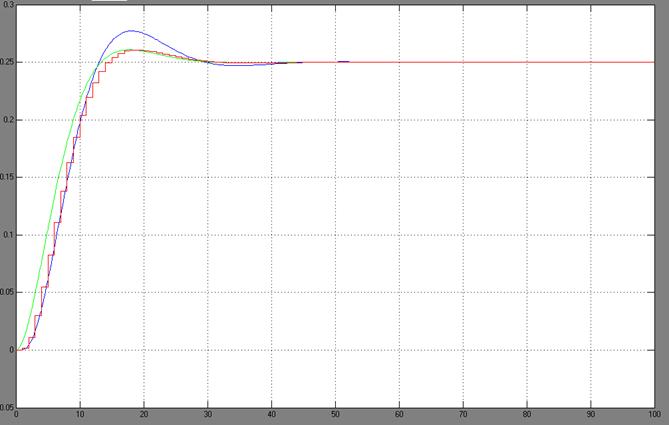
Рис.10. Желаемая ПХ до коррекции () (зеленая), желаемая скорректированная ДПХ (красная) и ПХ замкнутой системы с цифровым регулятором и исходным ОУ (синяя)

Из рис.10 видно, что динамика ОУ, неучтенная при синтезе ЦР, несущественно влияет на переходный процесс спроектированной замкнутой дискретной системы.

Литература

1. Лекции по курсу «Синтез законов управления в технических системах».

2. Медведев В.С., Потемкин В.Г. Control System Toolbox. Matlab 5 для студентов/ Под общ. ред. В.Г.Потемкина. – М.: ДИАЛОГ – МИФИ, 1999. – 287 с.