где s¢h – напряжения на основной площадке земляного полотна от воздействия расчетной шкалы под ее осью на глубине h от нижней постели;
s¢hc – напряжение в той же самой точке от давления (воздействия) соседней шкалы (находящейся слева от расчетной)
s²hc – то же, от давления соседней шкалы (находящейся справа от расчетной)
Каждое из этих напряжений есть функция от напряжений в балласте:
- по расчетной шпалой sБ
- под шпалой расположенной слева s¢бс
- под шпалой расположенной справа от расчетной s²бс
- от толщины балластного слоя h
![]()
Напряжения s¢h, s¢hc, s²hc определяются по формулам:
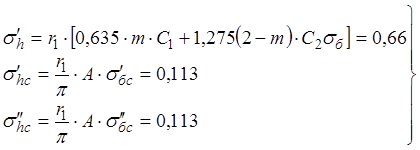
где ![]()
поправочный коэффициент r1=0,8 (для деревянных шпал); r1=0,7 (для железобетонных шпал);
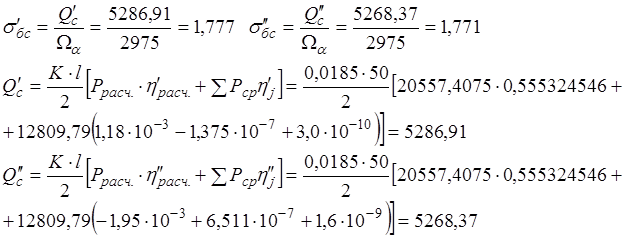
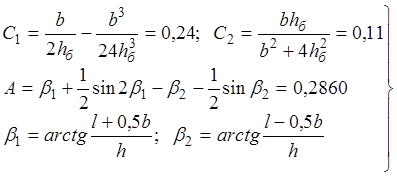
где b – ширина шпалы, см;
h – глубина, на которой определяется величина напряжения h³15
l – расстояние между осями шпал
b1 – угол между вертикалью и прямой, соединяющей начало полосовой нагрузки (эпюры напряжений) с точкой, в которой определяется напряжение
b2 - угол между вертикалью и прямой, соединяющей конец полосовой нагрузки с точкой
j- номер нагрузки, величина которой равна среднему значению, т.е. Pj=Pcp
Значения С1, С2 и А зависят от толщины балласта
Для вычисления наибольшей величины напряжения на основной площадке земляного полотна следует поочередно ставить каждую ось (нагрузку) в расчетное сечение по оси расчетной шкалы, предполагая при этом, что нагрузка от колеса находящегося над точкой А будет наибольшей, т.е. равная расчетной.
В этом случае необходимо каждый раз при новом положении расчетной нагрузки вычислять напряжения под нижней постелью соседних шпал с расчетной и самой расчетной шпалы.
При каждом загружении определяется суммарное напряжение и сравнивается с ранее полученным.
Напряжение на основной площадке земляного полотна определяется только от временной нагрузки, с учетом типов и числа обращаемых вагонов каждого типа.
Условия устойчивости бесстыкового пути против выброса определяются значением критических сжимающих сил в рельсовых плетях.
Величина критической силы может быть подсчитана по формулам К.Н. Мищенко, С.П. Першина или определена по экспериментальным данным (графикам или эмпирическим формулам) Е.М. Бромберга.
На основании экспериментальных исследований, выполняемых на экспериментальном пути-стенде во ВНИИЖТе под руководством Е.М. Бромберга получена эмпирическая зависимость допустимой предельной температурной силы для типовых конструкций бесстыкового пути с учетом плана линии.
![]()
где [Nк]¥ - критическое значение предельной силы, допускаемой на прямом участке пути;
h1 - коэффициент, учитывающий тип рельса;
h2 - коэффициент, учитывающий эпюру шпал;
А - коэффициент, зависящий от типа рельса и эпюры шпал;
R - радиус кривизны оси путевой решетки, м
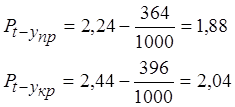
После вычислений максимально-допустимых значений температурных продольных сил по формуле Е.М. Бромберга вводить в расчет коэффициенты неопределенного запаса не надо. Соответствующее допустимое повышение температуры рельсовых плетей по сравнению с температурой их закрепления по условию обеспечения устойчивости против выброса определяются по формуле
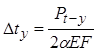
где a - температурный коэффициент линейного расширения рельсовой стали, равный 11,8×10-6 град-1.
F - площадь поперечного сечения одного рельса.

Температурное напряжение st (МПа), т.е. напряжение, которое возникает в рельсовой плети в связи с несостоявшимся изменением ее длины при изменении температуры на величину Dt, относительно температуры, при которой рельсовая плеть была закреплена, определяется по формуле
![]()
где a - температурный коэффициент линейного расширения рельсовой стали, равный 11,8×10-6 град-1.
Е - модуль упругости рельсовой стали, равный 2060000 МПа (2,1×106 кг/см2);
Dt - разность между температурой рельса, при которой определяют напряжение tр и температурой закрепления плети на шпалах tз, °С.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.