Прочность рельсовых плетей определяют из условия, чтобы сумма напряжений sк, возникающих от воздействия подвижного состава (с учетом коэффициента неучтенных факторов - коэффициента запаса прочности), и напряжений st, появляющихся в результате изменения температуры рельса, не превышала допустимого напряжения [sp0,2], т.е.
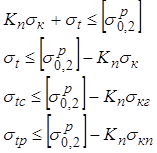
где sкг и sкп - нормальные напряжения в кромках соответственно головки и подошвы рельса от изгиба и кручения его под нагрузкой от колес подвижного состава;
stc и stp - напряжения в поперечном сечении рельса соответственно от действия сжимающих и растягивающих температурных сил, возникающих при повышении и понижении температуры рельса по сравнению с температурой при закреплении;
Кп - коэффициент запаса прочности, равный 1,3;
[sp0,2] » 343 МПа для нетермообработанных рельсов и
[sp0,2] » 392 МПа для термообработанных рельсов
Напряжение sкг определяется для зимних условий эксплуатации, sкп - для летних условий.
Наибольшее допустимое по условию прочности изменение температуры рельсовой плети по сравнению с ее температурой закрепления в сторону понижения (по условию прочности и подошвы рельса) равно
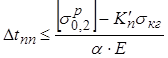
в сторону повышения (по прочности головки рельса)
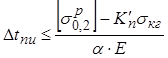
Расчетные допустимые понижения Dtр и повышения Dtс температуры рельсовой плети определяют с учетом условий
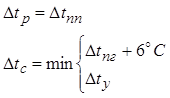
Данное выражение означает то, что допустимая величина изменения температуры рельсовой плети при действии сжимающих сил определяется минимальными значением, полученным либо по условию прочности Dtпг +6°С, либо по условию устойчивости пути против выброса Dtу.
Здесь 6°С – повышение температуры по сравнению с расчетной для снятия ограничения по укладке пути за счет повышения температурных напряжений в головке рельса при максимальных температурах в данном районе.
В зависимости от температурной работы различают рельсы «обычной длины», «длинные» и «бесстыковые рельсовые плети».
Рельсы обычной длины такие, удлинение и укорочение которых при изменениях температуры в пределах амплитуды многолетних колебаний температур ТА полностью за счет стыковых зазоров. При стыковых зазорах 19 и 21 мм при ТА³85°, рельс длины 25 м почти всегда нельзя отнести к рельсам «обычной длины». На дорогах СНГ ТА=78¸120°С, поэтому рельсы «обычной длины» или нормальной длины бывают длиной как 25,0 м, так и 12,5 м.
Длинными принято называть рельсы, у которых стыковой зазор равен нулю при температуре меньше, чем максимальная, в данном районе. Дальнейшее повышение температуры приводит к нажатию рельсов в стыке и появлению дополнительных продольных сил, определяемых разностью температур, при которой зазор равен нулю и максимальной. Поэтому необходимо рассчитывать устойчивость пути , уложенного длинными рельсами. При наиболее низких температурах при длинных рельсах стыковые болты, как правило, работают на срез (в особенности в кривых R<400 м).
Наибольшую возможную длину рельсов звеньевого пути можно определить по формуле, приведенной Лященко В.Н.
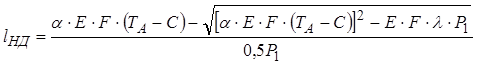
где a, Е – прежние значения;
F – площадь поперечного сечения рельса, см2;
С=2Dtн – для рельсов нормальной длины
l - величина зазора, см.
где 
- максимальный
конструктивный зазор, =23 мм (Р65) при диаметре болтовых отверстий 36 мм, =27,0 мм при диаметре болтовых отверстий 40
мм.
Р1 – величина погонного сопротивления перемещению рельса по одной рельсовой нити, кг/см, для костыльного скрепления Р1=6,4 кг/см при 32 парах противоугонов на 25 м звене на нетормозных участках пути; для пути клемными скреплениями Р1= 10кг/см.
1. Шахунянц Г.М. Железнодорожный путь. - М.: Трансжелдориздат, 1961
2. Проектирование железнодорожного пути. - 1972.
3. Шраменко В.П., Белорусов А.И. Расчет геометрических характеристик одиночных обыкновенных стрелочных переводов/ методические указания. - Харьков: ХИИТ, 1992.
4. Белорусов А.И. Расчет железнодорожного пути на прочность и устойчивость/ методические указания. - Харьков: ХИИТ, 1996. - Ч.1, 2.
5. Э.И. Даниленко, Расчет железнодорожного пути на прочность и устойчивость, Киевский институт жд. транспорта, 2000
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.