Методика индицирования дифрактограмм химических элементов с кубической элементарной ячейкой. Прецизионное измерение периода кубической элементарной ячейки

Цель работы:

               Ознакомление с принципом и методикой графического и аналитического индицирования порошковых дифрактограмм простых кристаллических вещёств с кубической элементарной ячейкой, способами отсчёта углового положения дифракционных линий, принципами прецизионного определения периода методами графической и аналитической экстраполяции.

Принцип и методика индицирования.

               Одной из задач структурного анализа является определение периода элементарной ячейки исследуемого кристаллического образца. В случае кубической сингонии можно воспользоваться выражением , где a – период ячейки; d – межплоскостное расстояние семейства параллельных атомных плоскостей с индексами Миллера (hkl). С учётом уравнения Вульфа-Брэгга это соотношение можно переписать так, что период может быть рассчитан  на основе дифрактограммы: 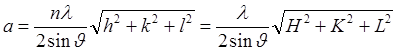, где l - длина волны характеристического рентгеновского излучения; J - угол дифракции; H = n×h, K = n×k, L = n×L – индексы отражения; n – порядок отражения от плоскостей (hkl). Зная индексы HKL данной линии, можно определить за счёт отражения какого порядка и от каких плоскостей получилась данная линия.

               Таким образом, измерив угол дифракции, можно определить период, если известны длина волны используемого излучения и индексы отражения HKL. Процедура нахождения индексов отражения каждой линии называется индицированием. Она основана на закономерностях погасания отражений с определённым сочетанием индексов HKL, зависящих от типа рассеивающих базисных атомов элементарной ячейки, их числа и расположения. Эти индексы могут быть найдены из условия равенства нулю структурной амплитуды F_HKL, которая учитывает фазовые соотношения между волнами, рассеянными различными базисными атомами:

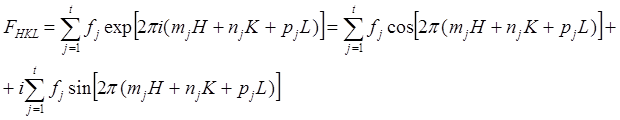
где f_j – атомная амплитуда рассеяния рентгеновского излучения j – м атомом; m_j, n_j, p_j – координаты базисных атомов; HKL – индексы отражения. Суммирование ведётся по всем t базисным атомам элементарной ячейки. Задав тип структуры, можно установить законы погасания.

               Используя данные по вычислению структурных амплитуд, можно заранее найти индексы HKL для кристаллов любого структурного типа кубической сингонии , для которых F_HKL¹0. Знание установленных таким образом закономерностей позволяет решить задачу индицирования.

               Уравнение Вульфа-Брэгга для i-той дифракционной линии образца с кубической структурой может быть записано в виде  .

               Тогда по отношению к первой линии на дифрактограмме получим . Ряд значений Q_i может быть вычислен для различных типов кубических структур на основе известных законов погасания тех или иных линий.

               Задача индицирования, в конечном счёте, сводится к последовательному сопоставлению экспериментальных значений для всех отражений одной длины волны излучения с теоретическими. Если нет грубых промахов, то различие состоит во второй десятичной значащей цифре. Также важно правильно определить индексы отражения первой линии. После установления типа структуры каждой линии следует присвоить соответствующий индекс отражения HKL.

               Кроме указанного выше способа аналитического индицирования в ряде случаев полезно и удобно использовать метод графического индицирования. Для графического индицирования необходимо построить график в координатах sinJ - l/a. При построении задают исходя из реальных значений a и l и удобства масштаба l/a и, последовательно меня сочетание индексов HKL так, чтобы сумма их квадратов менялась от 1 приблизительно до 20, получают семейство прямых на исходном графике. Далее на полоску бумаги наносятся в масштабе исходного графика значения sinJ_э полученные и дифрактограммы. Затем эту полоску бумаги перемещают так, чтобы нулевая точка полоски скользила по оси абсцисс, а сама полоска оставалась параллельной оси ординат. Перемещение производят до тех пор, пока все метки на полоске одновременно не совпадут в пределах погрешности с некоторыми  линиями на графике. Это положение  фактически и есть графическое решение уравнения  при двух неизвестных: периоде a и индексах отражения. Оно позволяет определить индексы, которые читаются на соответствующих прямых и период из отсчёта l/a на оси абсцисс при известной длине волны. Правильность найденных индексов следует проверить по известным законам погасания.

               Исходными данными, как для аналитического, так и для графического индицирования являются углы дифракции. Поэтому очень важно, в целях минимизации погрешности, правильно определять угловое положение дифракционных линий.

Методика определения углового положения дифракционной линии.