Учёт систематических погрешностей определения периода по дифрактометрическим данным. Источники систематических погрешностей различных методов дифрактометрии изучены достаточно хорошо. Некоторые из них, например погрешность определяемая преломлением рентгеновских лучей, остаются постоянными во всём диапазоне углов J, другие, наиболее существенные меняются по величине с углом J. Ниже приводятся угловые зависимости для основных погрешностей.
Смещение поверхности плоского образца от фокусирующей поверхности в схеме Брэгга-Брентано вызывает смещение центра тяжести равное DJ=-(g2ctgJ)/12, где g - горизонтальная расходимости первичного пучка излучения. Такое смещение приводит к дополнительной погрешности определения периода, Dа/а ~ ctg2J ~ cos2J.
Смещение поверхности образца от оси гониометра на величину S вызывает смещение центра тяжести, равное (S×cosJ)/Rг. Следовательно Dа/а ~ cosJ×ctgJ ~ cos2J.
Можно ещё привести целый ряд причин возникновения систематической погрешности, как геометрической так и физической природы. Это вертикальная расходимость рентгеновского пучка, проникновение излучения в образец (равносильно смещению образца от оси гониометра) и др. Важным для прецизионных измерений является установление функции, выражающей зависимость величины систематической погрешности данного типа от угла дифракции J. Это предпочтительнее, нежели расчёт индивидуальной поправки для каждого отражения.
Учёт систематических погрешностей экстраполяционными методами. Анализ систематических погрешностей показывает, что большинство из них стремится к 0 при J ® 900. Экспериментально измерить прецизионное значение периода, отвечающего углу J=900, невозможно, поэтому его находят экстраполяцией. Существует несколько методов экстраполяции. Рассмотрим некоторые из них.
Метод
аналитической экстраполяции. Данный метод на ряду с исключением систематических
погрешностей, позволяет свести к минимуму случайные. Для объёктивного
построения прямой, усредняющей величины полученные в ходе эксперимента, в
теории статистических решений используется общий метод нахождения параметров
прямой, при которых результаты наблюдения наиболее вероятны – принцип
максимального правдоподобия. В предположении что ошибки имеют нормальное
распределение, принцип максимального правдоподобия приводит к необходимости
отыскания решений, обеспечивающих минимум функции вида 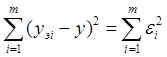 ,
где m – общее число экспериментальных точек; yэi
– экспериментально определённое i-тое значение параметра; y – истинное
значение параметра; ei
– случайная погрешность. Искомая величина может быть найдена из условия
минимума суммы квадратов невязок ei. Метод основанный на анализе данного уравнения носит
названия метода наименьших квадратов.
,
где m – общее число экспериментальных точек; yэi
– экспериментально определённое i-тое значение параметра; y – истинное
значение параметра; ei
– случайная погрешность. Искомая величина может быть найдена из условия
минимума суммы квадратов невязок ei. Метод основанный на анализе данного уравнения носит
названия метода наименьших квадратов.
Аналитическое
выражение графика линейной экстраполяции может быть записано в виде ![]() , где f(Ji) – значения
экстраполяционной функции для угла дифракции Ji. В – коэффициент пропорциональности определяющий
наклон прямой. Фактически B×f(Ji) –
систематическая погрешность нахождения периода по данному отражению. Т.к.
присутствует случайная ошибка то следует записать: aэi-a-B×f(Ji)=ei, и условие МНК имеет вид
, где f(Ji) – значения
экстраполяционной функции для угла дифракции Ji. В – коэффициент пропорциональности определяющий
наклон прямой. Фактически B×f(Ji) –
систематическая погрешность нахождения периода по данному отражению. Т.к.
присутствует случайная ошибка то следует записать: aэi-a-B×f(Ji)=ei, и условие МНК имеет вид 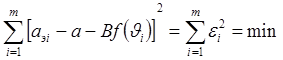 ,
чтобы данное условие было выполнено необходимо чтобы первые частные производные
по а и В были равны 0.
,
чтобы данное условие было выполнено необходимо чтобы первые частные производные
по а и В были равны 0.
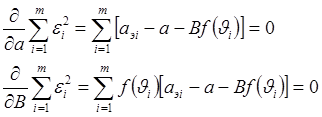
Раскрывая скобки и группируя члены, можно получить
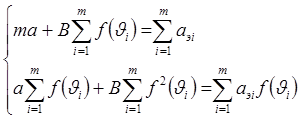
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.