Методика индицирования дифрактограмм химических элементов с кубической элементарной ячейкой. Прецизионное измерение периода кубической элементарной ячейки, страница 5

Здесь m – число рассматриваемых дифракционных отражений. Решая данную систему, находят точное значение периода, свободное от систематических погрешностей, определяемых видом f(J) при минимальном влиянии случайных. Исходными данными для расчёта являются: m – число анализируемых линий; l - длина волны характеристического рентгеновского излучения; J_i , H_iK_iL_i – угол дифракции и индексы отражения i-той линии; f(J) – вид экстраполяционной функции. Если угол J соответствует  положению центра тяжести дифракционной линии, то значение длины волны l при расчёте должно соответствовать центру тяжести спектральной линии используемого излучения.

               Представленный аналитический метод не учитывает, что измерение углового положения линии выполнено с различной степенью точности. Более верной была бы запись исходного уравнения в виде 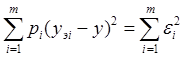, где p_i – вес i-того отражения, учитывающий неравноточность исходных экспериментальных данных, величина обратная дисперсии. , где s_i – среднеквадратическая ошибка данного измерения, а s₀ – коэффициент, используемый для нормировки веса, имеющий смысл среднеквадратичной ошибки на единицу веса. Учитывая что s_i ~ ctgJ_i, целесообразно приписывать отражению вес, пропорциональный tg²J_i. В то же время ясно, что погрешность в определении углового положения наиболее интенсивной линии минимальна. Тогда  вес наиболее интенсивной линии можно принять за единицу, а другим линиям условно присвоить вес V_i в долях этой единицы. Тогда в качестве весовой функции удобно использовать p_i = V_i×tg²J_i.

Обработка результатов измерений по прецизионному определению периода ячейки.

1. Графическая экстраполяция

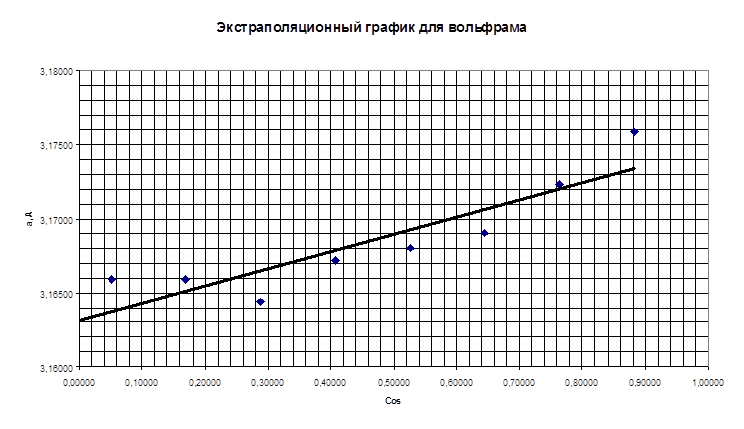
По графику можно определить а_гр=3,163А

2. Аналитическая экстраполяция

Исходные данные для экстраполяции:

В результате решения системы МНК были получены следующие результаты: a_ан = 3,16332А, В = 0,01152А

3. Оценка случайной погрешности

Случайная погрешность рассчитывается по формуле 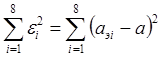= 3,34×10^-4A.

Выводы:

Аналитическое индицирование дифрактограммы позволяет однозначно указать тип кубической ячейки вещества. Однако и здесь присутствуют некоторые трудности т.к. некоторые линии регистрировались уже на уровне фона и точно сказать что данная линия там присутствует невозможно. Если упустить линию с малой интенсивностью, то, например, может получается что вольфрам имеет примитивную ячейку. Т.е. при всей точности метода возможны серьёзные промахи, зависящие в основном от «качества» исходных данных и внимательности экспериментатора.

При определении положения дифракционной линии были оценены зависимости точности расчёта центра тяжести от ширины интервала, предложенного для интегрирования. Полученная зависимость говорит о том, что чем лучше указать границы перехода линия – фон тем точнее будет определён центр тяжести.

При оценке зависимости точности определения центра тяжести от степени полинома аппроксимирующего фон, лучше всего себя показала линейная аппроксимация.

Полученное значение периода – а = 3,1633А хорошо согласуются с литературным значением периода ячейки для вольфрама а = 3,165А, но точность оказалась ниже ожидаемой.

При определении периода элементарной ячейки использовался метод не учитывающий веса отражения, что приводит к повышению ошибки.

Неточное определение периода также может быть связано с несовершенством структуры кристалла вольфрама, также с наличием примесей (образующих твёрдый раствор) в кристалле.