Задача синтеза и анализа дискретного фильтра

В основе цифровой фильтрации лежат преобразование аналоговых сигналов в последовательность чисел и обработка этой последовательности в цифровом вычислительном устройстве, роль которого может играть как универсальная ЭВМ, так и специализированный цифровой процессор.

Применение цифровой фильтрации в радиоэлектронике открывает дополнительные возможности при обработке сигналов. В частности, могут быть реализованы такие фильтрационные алгоритмы, которые аналоговыми методами вообще не осуществимы. В цифровой форме возможен синтез аналогов известных радиотехнических устройств различного функционального назначения: преобразователей частоты, детекторов и т. п. [1]–[7].

Настоящая курсовая работа дает студентам возможность приобрести и закрепить практические навыки в области дискретной и цифровой обработки сигналов на примере решения конкретной задачи синтеза и анализа дискретного фильтра.

1. ЗАДАНИЕ

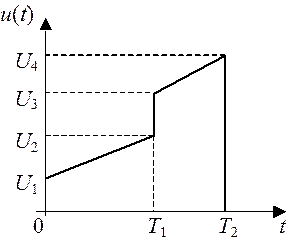1. В качестве входного сигнала в курсовой работе рассматривается дискретизированный видеоимпульс x(kT), где T — интервал дискретизации; пример исходного аналогового сигнала u(t), заданного на интервале [0, T₂] двумя отрезками прямых, показан на рисунке.

Входной сигнал задается с вариацией параметра T₁, принимающего в каждом индивидуальном задании три конкретных значения.

2. В качестве шумового сигнала в курсовой работе рассматривается стационарный случайный дискретный процесс , представляющий собой последовательность отсчетов, являющихся значениями непрерывной нормально распределенной случайной величины  с заданными значениями математического ожидания  и дисперсии . Здесь T — интервал дискретизации, а  — среднеквадратичное значение .

3. Задание на курсовую работу заключается в следующем:

а) рассчитать спектральные функции для трех вариантов заданного входного сигнала, выбрать по указанному в индивидуальном задании критерию один из них и провести его дискретизацию;

б) методом билинейного z‑преобразования синтезировать дискретный фильтр (ДФ) нижних частот (ФНЧ) с частотой среза , где  — частота, на которой уровень амплитудного спектра  выбранного входного видеосигнала снижается до уровня  спектра выбранного входного сигнала u(t). При этом в зависимости от индивидуального задания в качестве аналогового прототипа используется фильтр одного из двух типов:

·  ФНЧ с максимально плоской амплитудно-частотной характеристикой (АЧХ) — фильтр Баттерворта, обеспечивающий на удвоенной частоте среза аналогового фильтра  затухание не менее a дБ;

·  ФНЧ с равноволновой в полосе пропускания АЧХ — фильтр Чебышева с неравномерностью b дБ, позволяющий, как и в первом случае, на частоте  получить затухание не менее a дБ;

в) рассчитать амплитудно-частотную и импульсную характеристики синтезированного ДФ;

г) определить вид дискретных сигналов на выходе фильтра при воздействии на его вход последовательности отсчетов входного сигнала x(kT), а также двух-трех сигналов стандартной формы (заданных преподавателем);

д) выполнить анализ прохождения через синтезированный фильтр случайного дискретного сигнала с оценкой его математического ожидания, дисперсии, корреляционной функции и интервала корреляции на входе и выходе ДФ. Исследовать фильтрацию аддитивной смеси исходных дискретных детерминированного и случайного сигналов при различных значениях отношения сигнал/шум на входе ДФ.

Задание может быть представлено в виде таблицы по приведенному выше образцу.

2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И КОММЕНТАРИИ

Дискретным сигналом x(kТ) называется последовательность отсчетов непрерывного сигнала x(t), взятых в моменты времени kT (k = 0, 1, 2, ...); T — интервал дискретизации. Предполагается, что x(t) º 0 при t < 0. В ДФ над элементами данной последовательности в согласии с заданным алгоритмом обработки осуществляются операции сложения, вычитания, умножения и задержки во времени, в результате чего на выходе фильтра формируется новый дискретный сигнал.

Отличительной особенностью цифровой обработки является квантование дискретного сигнала по уровню, необходимое для перевода его значений в числовую последовательность и преобразования ее в вычислительном устройстве — цифровом фильтре. Предметом рассмотрения в настоящей курсовой работе служат исключительно дискретные сигналы и фильтры, так как в основе анализа цифровых и дискретных устройств лежит один и тот же математический аппарат — теория линейных дискретных систем, а учет эффектов квантования представляет собой самостоятельную и сложную задачу.