Задача синтеза и анализа дискретного фильтра, страница 3

Это означает, что при использовании метода билинейного z‑пре­об­ра­зо­ва­ния необходимо привести в соответствие частотные характеристики синтезируемого дискретного фильтра и аналогового фильтра-прототипа. Приближенный характер рассмотренного метода синтеза, даже с учетом трансформации частотной оси, позволяет реализовать частотную характеристику прототипа с некоторой погрешностью, исчезающей лишь в том случае, когда исходная частотная характеристика имеет вид ступенчатой функции.

3. ПОРЯДОК ВЫПОЛНЕНИЯ КУРСОВОЙ РАБОТЫ

3.1. Расчет спектральной плотности входного сигнала

С помощью программы FILTER рассчитайте амплитудные спектры заданных вариантов входного сигнала. Расчет произведите в диапазоне, который ориентировочно можно оценить, исходя из того факта, что ширина главного лепестка спектра прямоугольного видеоимпульса длительности  равна 1/; целесообразно задать частотный интервал ~ 3/. Результаты расчета сведите в таблицу и постройте соответствующие графики.

Определите верхние граничные частоты  спектров заданных входных сигналов по критерию уменьшения их амплитудных спектров до уровня 0,1 от максимального значения амплитудного спектра S(0). Для этого ориентировочно оцените частотные интервалы, в которых находятся интересующие вас частоты. Затем, используя программу FILTER, определите точные значения соответствующих граничных частот.

Выберите вариант сигнала, которому отвечает наибольшее (max), наименьшее (min) или среднее (mid) значение граничной частоты (в соответствии с индивидуальным заданием). В дальнейшем рассматривается только этот вариант сигнала.

Выведите аналитическое выражение для спектральной функции выбранного входного сигнала. При выводе можно использовать известный метод дифференцирования (в данном случае двукратного) кусочно-линейной функции u(t) и вычисления спектральной функции производной с последующим интегрированием в спектральной области либо непосредственно применить интеграл Фурье. Получите расчетные соотношения для амплитудного спектра, вещественной и мнимой составляющих спектра и фазового спектра выбранного входного сигнала и выведите соответствующую таблицу в пределах f_0,1. Постройте графики вещественной и мнимой составляющих спектра, график фазового спектра сигнала. Используя полученные аналитические выражения, «вручную» рассчитайте значения амплитудного и фазового спектров в трех контрольных точках (на нулевой и двух произвольно выбранных в пределах f_0,1 частотах), задав их таким образом, чтобы обеспечить возможность сопоставления результатов с данными, полученными при машинном расчете. При расчете значения  требуется раскрытие неопределенности по правилу Лопиталя. Для самоконтроля полезно представить спектральную функцию сигнала в виде  и использовать вытекающие из прямого преобразования Фурье

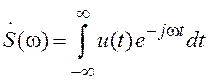
соотношения:

                                ,

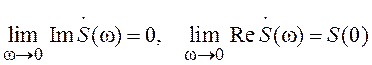где 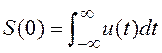 — «площадь» входного сигнала u(t) в системе координат «время — сигнал».

3.2. Дискретизация непрерывного входного сигнала

Последовательность отсчетов входного дискретного сигнала рассчитывают, исходя из теоремы отсчетов (теоремы Котельникова), которая гласит: если значение наивысшей частоты в спектре сигнала x(t) меньше, чем , то данный сигнал полностью определяется последовательностью своих отсчетов в моменты времени, отстоящие друг от друга не более, чем на интервал .

Непосредственное применение теоремы невозможно, так как ограниченный во времени (финитный) входной сигнал x(t) имеет бесконечно протяженный спектр. Поэтому за наивысшую, , принимают частоту , которая была определена в 3.1. Интервал дискретизации выбирают, учитывая также требования к погрешностям дискретизации и восстановления непрерывного сигнала. Учет этих требований выходит за рамки курсовой работы; практически при определении интервала дискретизации необходимо в соотношении

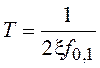
подобрать коэффициент x таким образом, чтобы на длительность входного сигнала T₂ приходилось не менее 20–25 отсчетов.

Осуществив дискретизацию сигнала x(t), необходимо построить график последовательности отсчетов входного сигнала x(kT), а также график амплитудного спектра дискретизированного сигнала , используя соотношение [1]